Moment Problem

Choose an exact function

> exact_function := exp(x)+exp(-x)*cos(11*x):

Choose the highest index for the moments to be computed

> N := 24;

Compute the exact moments

> for i from 0 to N do exact_moment[i] := int(x^i*exact_function,x=0..1); od:

Compute numerical approximations to the exact moments

> for i from 0 to N do approx_moment[i] := evalf(exact_moment[i],100); od:

> model_function := add(c[i]*x^i,i=0..N):

Compute the left hand sides of the moment equations

> for i from 0 to N do eq[i] := int(x^i*model_function,x=0..1); od:

Look at the coefficients in the left hand side of the first equation

> seq(coeff(eq[0],c[i]),i=0..N);

and look at the coefficients in the left hand side of the last equation.

> seq(coeff(eq[N],c[i]),i=0..N);

We recognize the first row and last row of Hilbert's matrix.

Define the set of equations.

> eqs := {seq(eq[i]=approx_moment[i],i=0..N)}:

Numerically solve the equations with 16 digits precision.

> Digits := 16:

> s16 := fsolve(evalf(eqs)):

> p16 := sort(subs(s16,model_function));

Plot the error between the exact function and approximate solution p16.

> plot(exact_function-p16,x=0..1);

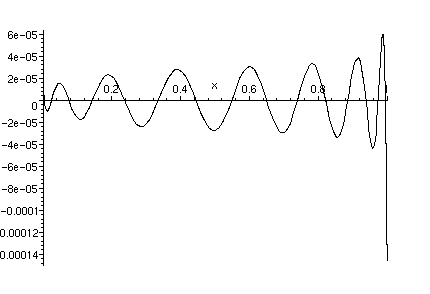
Try again at 32 digits.

> Digits := 32:

> s32 := fsolve(evalf(eqs)):

> p32 := sort(subs(s32,model_function));

> plot(exact_function-p32,x=0..1);

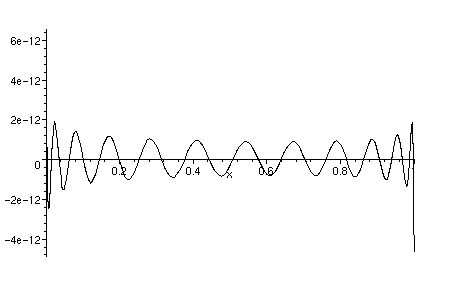
Now we see that the error is about 7 orders of magnitute smaller.