CECM Home > Interfaces
Interfaces
README: These interfaces were developed in the 1990s. Some are running on our old web server "oldweb.cecm.sfu.ca", an ancient SGI workstation running IRIX. Some have been ported over to Linux and are running on a Red Hat web server "wayback.cecm.sfu.ca". Some no longer work. Sorry.
|
Viet Elser's Phase Retrieval |
|
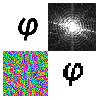
|
Phase retrieval is an inverse problem that arises in several disciplines. This site has been created to stimulate the development of phase retrieval algorithms by offering a selection of problems that challenge the state-of-the-art. |

|
Based on JavaView, a 3D visualization and manipulation package, this interface allows one to import and export Maple plot structures and enhance them. The software is downloadable and for PC's. Enjoy the Java Gallery that sits on top of it. |
|
To determine linear integer dependence among numerical constants and to determine the minimal polynomial of an approximate algebraic number. |
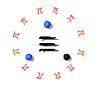 |
The story of pi reflects the most seminal, the most serious and sometimes the silliest aspects of mathematics. A surprising amount of the most important mathematics and a significant number of the most important mathematicians have contributed to its unfolding … |
|
Rob Scharein's KnotPlot |
|
 |
Here you will find a collection of knots and links, viewed from a (mostly) mathematical perspective. Nearly all of the images here were created with KnotPlot, a fairly elaborate program to visualize and manipulate mathematical knots in three and four dimensions. |
|
The Colour Calculator: an interactive tool |
|
 |
This model on-line laboratory is designed for exploration of number theory through visualization with symbolic and numeric engine support. |

|
Similar to the Colour Calculator mentioned previously, the Java version uses OpenMath JavaBeans to interconnect the functionalities provided by remote and local services. |
 |
This interface is designed for evaluation of Euler sums, based on our fast method of turning them into convolution of geometrically converging nested sums. |
 |
This is a Java interface for evaluation of Euler sums. |
 |
In addition to calculating Euler sums as described previously, this interface also evaluates related sums. |
 |
This interface was developed as part of the Organics Mathematics Project. As of January 1 1998, access to Maple V release 3 via the Maple Form Interace (MFI) is restricted to users covered by Simon Fraser University's campus license. Waterloo Maple Inc has until now graciously allowed us to provide free access to our copy of Maple for use within the Organics Mathematics Proceedings. At this time, we must observe the letter of our campus license and limit access appropriately. Users with a valid Maple license and/or who belong to SFU's campus and wish to utilize the MFI interface may contact CECM directly. |
 |
This interface can predict exactly which card you are going to turn over! |
 |
This interface lets you visualize the entries of Pascal's triangle with respect to a modulus between 2 and 16. |
 |
The Organic Mathematics Project (OMP) is directed towards the exploration of the emerging network and information technologies within the context of mathematics. |
 |
The MomEnt+ project is a computational engine intended to implement and expand the applicability of much of the maximum entropy theory that has been developed in the past few years. The project is not a single package or piece of code, but rather a diverse combination of computer programs, theories, and contacts, designed to enhance the participants' collective knowledge of numerical optimization … |
 |
The ISC is a set of programs and specialized tables of mathematical constants, dedicated to the identification of real numbers. It also serves as a way to produce identities with functions and real numbers. It is one of the main ongoing projects at CECM. |
 |
This interface allows you to calculate, on-the-fly, all roots of polynomials with coefficients of either 0 and 1 or -1 and 1. The software permutes through all possible combinations of polynomials, solving for the roots of each. Then, all roots are plotted on the complex plane (around the origin). |
 |
This isn't a web interface but more in the nature of an OpenMath library. |