![[Shownotes]](../gif/annotate/shide-101.gif)
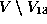 are
are 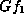 ,
, 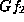 , and
, and
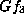 . We do this by counting the G-orbits in the vector space V over
the finite field
. We do this by counting the G-orbits in the vector space V over
the finite field 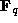 ,
of order
,
of order 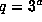 , for every
, for every 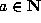 . We use estimates of the number
of such points for orbits of a specific dimension to show there are
no further orbits of dimension 14 or higher.
. We use estimates of the number
of such points for orbits of a specific dimension to show there are
no further orbits of dimension 14 or higher.
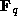 but
become
equivalent when viewed as forms over k.
We are assuming here that
but
become
equivalent when viewed as forms over k.
We are assuming here that 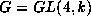 where k is the algebraic
closure of
where k is the algebraic
closure of 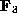 , and that
, and that 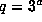 for some a.
for some a.
Let 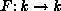 be the Frobenius map which raises elements to the q-th power, and
let it act entrywise on G. The set of fixed points under F in G
is
be the Frobenius map which raises elements to the q-th power, and
let it act entrywise on G. The set of fixed points under F in G
is 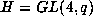 of order
of order

 Let W be the
16-dimensional vector space of forms modulo cubics we have been
analyzing, but now defined over
Let W be the
16-dimensional vector space of forms modulo cubics we have been
analyzing, but now defined over 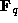 , so that
, so that 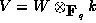 .
We want to consider an orbit Gf say of the form f. We
assume here that f has coefficients fixed by F; in other words,
they lie in
.
We want to consider an orbit Gf say of the form f. We
assume here that f has coefficients fixed by F; in other words,
they lie in 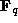 , which is the fixed field of F.
For f as in Table 1, they are in the ground field
, which is the fixed field of F.
For f as in Table 1, they are in the ground field 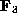 . We
will try to analyze the set Y of elements in Gf which are fixed by
F, that is,
. We
will try to analyze the set Y of elements in Gf which are fixed by
F, that is, 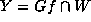 .
We are using the two actions of F on G and also on V.
Let
.
We are using the two actions of F on G and also on V.
Let 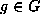 . If gf
has coefficients fixed by F, so does hgf for each
. If gf
has coefficients fixed by F, so does hgf for each 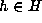 .
This means that the elements of H
act on Y and form orbits under this action. As
.
This means that the elements of H
act on Y and form orbits under this action. As 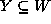 ,
the cardinality of Y is finite.
,
the cardinality of Y is finite.
Let R be the stabilizer in G of f and S its connected component.
Then 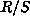 is finite, say of size n, so there
are coset representatives
is finite, say of size n, so there
are coset representatives 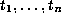 of S in R.
We assume that q has been
chosen so they are fixed by F. Assume
of S in R.
We assume that q has been
chosen so they are fixed by F. Assume 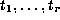 is a complete set of
representatives for the conjugacy classes of
is a complete set of
representatives for the conjugacy classes of 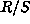 . We prove the following:
Theorem. There are exactly r orbits of H acting on Y.
The orbits are precisely
. We prove the following:
Theorem. There are exactly r orbits of H acting on Y.
The orbits are precisely
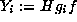 ,
, 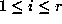 , where
, where 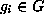 with
with
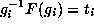 . Moreover, if
. Moreover, if
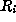 denotes the subgroup of R consisting of
all elements
denotes the subgroup of R consisting of
all elements 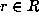 for which
for which 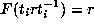 , the number
of elements in
, the number
of elements in 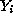 is
is 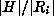 .
.
We proceed in five steps.
Notice first that 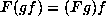 ,
as f has coefficients in
,
as f has coefficients in 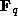 . It follows that
if
. It follows that
if 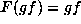 , then
, then
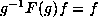 ,
and so
,
and so 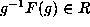 so
so 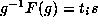 for
for
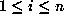 and
and 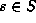 . Suppose on the other hand that
. Suppose on the other hand that
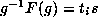 for some i,
for some i, 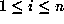 and s in S;
then
and s in S;
then 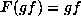 . This means that all elements in Y are of the
form gf for such a g.
B. For each i, there is
a
. This means that all elements in Y are of the
form gf for such a g.
B. For each i, there is
a 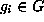 for which
for which 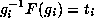 .
.
Lang's theorem applies to
G acting on itself as G is connected. The fixed points of
the automorphism F are finite and so there is a 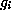 for which
for which
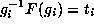 .
.
To see the converse suppose 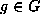 satisfies
satisfies
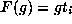 . Then
. Then
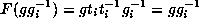 and so
and so 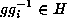 .
This means the coset
.
This means the coset 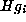 is exactly the set of elements g of
G for which
is exactly the set of elements g of
G for which 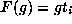 . There is one orbit of H in
Y given by
. There is one orbit of H in
Y given by 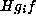 .
.
D. Suppose that 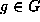 satisfies
satisfies
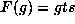 with
with 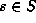 and
and 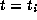 for some
i. Then
for some
i. Then 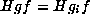 .
.
We will show that there exists
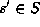 satisfying
satisfying 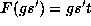 . Then
. Then
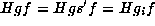 by C.
by C.
Notice that
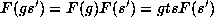 ,
and so we want to find
,
and so we want to find 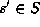 with
with
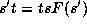 or, equivalently,
or, equivalently,

 Let
Let 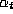 be conjugation by t acting on S by
be conjugation by t acting on S by
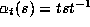 . The condition for
. The condition for 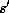 is
is


Let 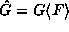 . Note that
since
. Note that
since 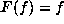 , the Frobenius map F stabilizes R and so S as well.
By Lang's theorem,
all elements in the coset FG are conjugate in
, the Frobenius map F stabilizes R and so S as well.
By Lang's theorem,
all elements in the coset FG are conjugate in 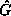 .
Thus
.
Thus
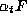 fixes only finitely many
points (indeed |H| points) on G and so also on S.
By Lang's theorem, applied to
fixes only finitely many
points (indeed |H| points) on G and so also on S.
By Lang's theorem, applied to 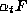 acting on S, there is such an
acting on S, there is such an 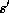 .
E.
For
.
E.
For 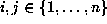 , we have
, we have
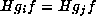 if and only if
if and only if 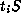 and
and 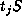 are conjugate in
are conjugate in 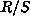 .
.
Suppose 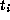 and
and 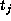 are conjugate in
are conjugate in 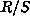 by an element
by an element
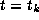 . This means
. This means 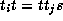 for
for 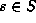 .
Then
.
Then 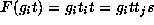 . From D.,
it follows that
. From D.,
it follows that 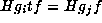 . Note that
. Note that 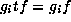 and so the
H-orbits of
and so the
H-orbits of 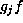 and of
and of 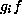 are the same.
are the same.
Suppose on the other hand that 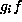 and
and 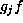 are in the same
H-orbit. We may assume
are in the same
H-orbit. We may assume 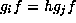 for some
for some 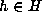 and
so
and
so 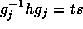 for one of the coset representatives t and
for one of the coset representatives t and
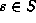 . Now
. Now 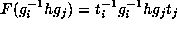 and so
and so
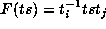 . But under F, the coset tS is mapped
to tS as S is mapped to S and so
mod S,
. But under F, the coset tS is mapped
to tS as S is mapped to S and so
mod S, 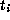 and
and 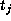 are conjugate.
This means we need only consider the orbits
are conjugate.
This means we need only consider the orbits 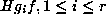 .
.
F. The only remaining part is to show that the number of
elements in the orbit of 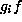 is as indicated. The stabilizer
in H of
is as indicated. The stabilizer
in H of 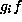 is exactly
is exactly 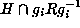 . But,
for
. But,
for 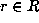 , the conjugate
, the conjugate 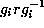 is in H if and only if it is fixed by F. This gives
is in H if and only if it is fixed by F. This gives
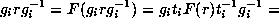 which is
equivalent to
which is
equivalent to 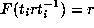 as given, that is,
as given, that is, 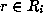 .
Corollary. Suppose the stabilizer R splits
as an extension over S (so that we can choose
the coset representatives
.
Corollary. Suppose the stabilizer R splits
as an extension over S (so that we can choose
the coset representatives
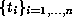 of S in R in such a way that they form a
group themselves fixed by F).
Then
of S in R in such a way that they form a
group themselves fixed by F).
Then


As above, let 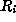 be the set of elements r in R
satisfying
be the set of elements r in R
satisfying 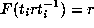 , so that
, so that 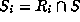 .
Suppose
.
Suppose 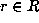 . Write
. Write
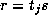 with
with 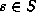 . Then
. Then 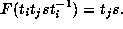 Because
we have chosen the
Because
we have chosen the 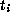 to be fixed by F,
this means
to be fixed by F,
this means 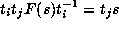 . But this
implies that
. But this
implies that 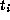 and
and 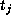 commute modulo S and so commute
as the
commute modulo S and so commute
as the 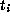 form a group.
This implies
form a group.
This implies 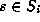 .
Thus,
.
Thus, 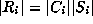 where
where
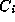 is the centralizer of
is the centralizer of 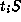 in
in 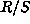 .
By the theorem, we now have
.
By the theorem, we now have
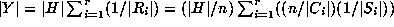 .
But
.
But 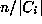 is the size of the conjugacy class and so the result
follows.
Corollary. If R is finite, then
|Y|=|H|.
is the size of the conjugacy class and so the result
follows.
Corollary. If R is finite, then
|Y|=|H|.
|S|=1 in the above.
Corollary. If 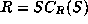 (in particular
if R=S), then
(in particular
if R=S), then
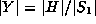 (where
(where 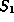 are the just the fixed
points of F on S).
are the just the fixed
points of F on S).
Any 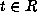 induces an inner
automorphism on S. It follows by Lang's theorem,
that
induces an inner
automorphism on S. It follows by Lang's theorem,
that 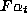 is conjugate to F by an element of S and so has the
same number of fixed points as F on S.
is conjugate to F by an element of S and so has the
same number of fixed points as F on S.
We now add the contributions to 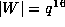 from the orbits of forms
from the orbits of forms 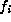 ,
, 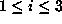 .
Note that the stabilizers in G of these forms are given in
.2. Here h=|H| is as in the beginning of this section.
For
.
Note that the stabilizers in G of these forms are given in
.2. Here h=|H| is as in the beginning of this section.
For 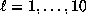 ,
we shall denote by
,
we shall denote by 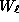 the set
the set 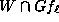 .
.
The stabilizer of 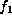 is finite and so, by Corollary 6.3,
the number of points in
is finite and so, by Corollary 6.3,
the number of points in 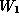 is h.
is h.
The stabilizer of 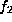 is
is 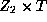 where T is a
one-dimensional
torus and
where T is a
one-dimensional
torus and 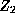 is the cyclic group of order 2
generated by the matrix
is the cyclic group of order 2
generated by the matrix 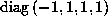 . There are two
orbits, each of size
. There are two
orbits, each of size 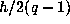 , so
, so 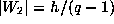 .
.
The stabilizer of 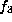 is connected and so the number of orbits is
one and the size is
is connected and so the number of orbits is
one and the size is 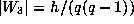 .
.
Now adding the contributions for these three orbits and subtracting
from 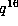 gives a polynomial of degree 13.
gives a polynomial of degree 13.
We now quote a result by [LW] which shows there are no more orbits of dimension 14 or higher.
Theorem. [LW]. Let X be a d-dimensional
subvariety of an n-dimensional projective space defined
over 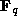 . There exists a constant c (depending only on
X, d and n - in fact, not on X explicitly, but
on the degree of X in the projective space)
. There exists a constant c (depending only on
X, d and n - in fact, not on X explicitly, but
on the degree of X in the projective space)
Note this result also works
for subvarieties of affine space.
For one direction, embed the affine variety in
projective space and consider the closure;
then 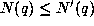 where
where 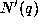 is the number
of
is the number
of 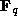 -points of the closure and use the upper bound
for that. For the other bound, choose an open subset O
contained in the original variety. Then the number of
-points of the closure and use the upper bound
for that. For the other bound, choose an open subset O
contained in the original variety. Then the number of 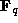 -points
on the closure
-points
on the closure 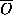 of O
and the complement of O in
of O
and the complement of O in 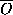 can be estimated, and so also
on O; this gives the appropriate lower bound for
can be estimated, and so also
on O; this gives the appropriate lower bound for 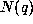 .
Corollary.
Theorem
.
Corollary.
Theorem  holds.
holds.
If 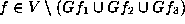 satisfies
satisfies 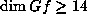 , then, by Theorem 6.5, the number of
, then, by Theorem 6.5, the number of 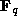 -points of Gf
(the only dense orbit of
-points of Gf
(the only dense orbit of 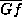 ) is at least
) is at least
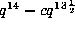 (for some constant c), which contradicts
the fact that the number of
(for some constant c), which contradicts
the fact that the number of 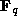 -points of
-points of 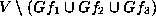 is a polynomial in q of degree 13. This shows
there are no further orbits of dimension 14 or higher. In
particular, all other orbits lie in
is a polynomial in q of degree 13. This shows
there are no further orbits of dimension 14 or higher. In
particular, all other orbits lie in 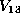 . In , any form in
. In , any form in
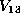 was shown to be listed in Table 1.
Our work is over the algebraic closure of
was shown to be listed in Table 1.
Our work is over the algebraic closure of 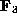 . However arguments
in [GLMS] show the same applies over any algebraically closed field of
characteristic 3.
. However arguments
in [GLMS] show the same applies over any algebraically closed field of
characteristic 3.