![[Shownotes]](../gif/annotate/shide-111.gif)
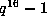 , showing again that
all forms have been accounted for.
, showing again that
all forms have been accounted for.
The H-orbits corresponding to 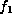 ,
, 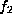 ,
, 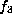 have been dealt
with
above. We now discuss the remaining forms individually.
The stabilizer of
have been dealt
with
above. We now discuss the remaining forms individually.
The stabilizer of 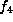 is a connected 3-dimensional
group with a 2-dimensional unipotent radical.
Thus,
is a connected 3-dimensional
group with a 2-dimensional unipotent radical.
Thus, 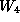 is a single H-orbit of size
is a single H-orbit of size
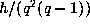 .
.
For 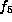 there are two orbits. An element representing the second
coset is given by
there are two orbits. An element representing the second
coset is given by 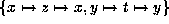 . The number of elements
in the orbit corresponding to the identity is
. The number of elements
in the orbit corresponding to the identity is 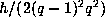 .
The number of elements in the orbit corresponding to the other
orbit is
.
The number of elements in the orbit corresponding to the other
orbit is 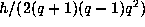 . This follows as the values of
. This follows as the values of
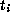 and
and 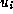 which satisfy the relations are
which satisfy the relations are
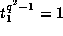 ,
, 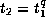 and
and 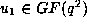 with
with
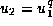 .
There is one orbit for
.
There is one orbit for 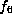 containing
containing 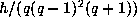 where
the denominator is the order of
where
the denominator is the order of 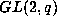 .
.
There are two orbits for 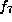 . The second is given by
. The second is given by
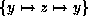 . The number in the first is
. The number in the first is
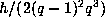 . The number in the second is
. The number in the second is
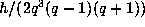 . This follows as the elements in S
acting in the appropriate manner are given by
. This follows as the elements in S
acting in the appropriate manner are given by
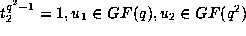 and the
relations
and the
relations 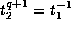 ,
, 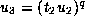 .
.
The remaining forms are in 3 variables. There are
three orbits for 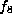 as in the case of three variables.
The contribution of the identity is
as in the case of three variables.
The contribution of the identity is 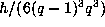 .
The contributions from the involution and the 3-cycle are
.
The contributions from the involution and the 3-cycle are
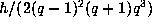 and
and 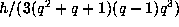 , respectively.
, respectively.
The remaining forms 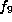 and
and 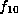 each have just one orbit,
of sizes
each have just one orbit,
of sizes 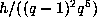 and
and 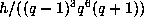 , respectively.
, respectively.