![[Shownotes]](../gif/annotate/shide-21.gif)
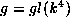 , the Lie algebra of all endomorphisms
of the vector space
, the Lie algebra of all endomorphisms
of the vector space 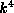 .
We shall use its basis
.
We shall use its basis 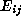 for
for 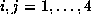 ,
where
,
where 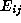 stands for the matrix with 1 at entry i,j and
0 elsewhere.
stands for the matrix with 1 at entry i,j and
0 elsewhere.
For simplicity of computations, we choose a basis
x,y,z,t of 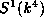 and let
and let 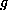 act
on
act
on 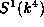 by the usual matrix action on column vectors
from the left.
Thus, for instance
by the usual matrix action on column vectors
from the left.
Thus, for instance

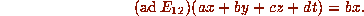 This then determines the action of
This then determines the action of 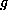 on
on 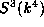 and hence the action on V.
For example,
and hence the action on V.
For example,


As a basis for V, we shall use the 16 monomials in x,y,z,t
which are not cubes.
Let us denote by 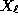 the
the 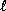 -th monomial in the second row of the
array
below.
-th monomial in the second row of the
array
below.
The action of 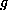 on V can now be explicitly given
in terms of the following matrix
on V can now be explicitly given
in terms of the following matrix 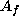 where
where 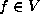 is written as
is written as

 Here
Here 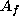 is the
is the 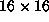 matrix
whose ij-th row consists of the coefficients of
matrix
whose ij-th row consists of the coefficients of
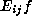 written out on the basis of V just given.
In the array below, the row beginning with
written out on the basis of V just given.
In the array below, the row beginning with 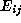 represents
the
ij-th row of
represents
the
ij-th row of 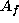 , that is, the
vector
, that is, the
vector 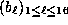 such that
such that
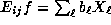 .
.

 For
For 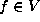 , we write
, we write 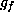 to denote the Lie subalgebra of
to denote the Lie subalgebra of 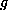 consisting of all
consisting of all 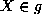 with
with 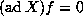 .
.
A major tool for discriminating orbits is the following
family of varieties 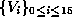 :
:

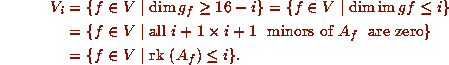 If f and
If f and 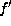 are equivalent by an element y in G,
then
are equivalent by an element y in G,
then 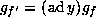 and so the dimensions of
and so the dimensions of
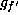 and
and 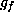 are the same. Hence all forms equivalent
to a given f are in the same
are the same. Hence all forms equivalent
to a given f are in the same 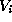 . Suppose
. Suppose 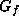 is the
stabilizer in G of a form f and
is the
stabilizer in G of a form f and 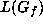 is its Lie algebra
in
is its Lie algebra
in 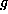 . Then
. Then 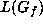 is a Lie subalgebra of
is a Lie subalgebra of 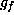 . This
gives that the
dimension of
. This
gives that the
dimension of 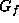 is at most the dimension of
is at most the dimension of 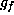 . Therefore,
the dimension of the orbit Gf of f is at least i if
f is in
. Therefore,
the dimension of the orbit Gf of f is at least i if
f is in 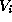 .
.