![[Shownotes]](../gif/annotate/shide-61.gif)
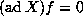 for
for 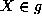 .
They are explicitly given below as linear subspaces of
.
They are explicitly given below as linear subspaces of 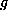 .
.







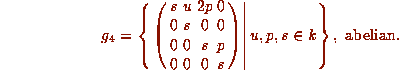



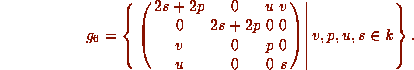 The commutator subalgebra
The commutator subalgebra
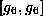 is perfect of dimension 3.
The radical of
is perfect of dimension 3.
The radical of 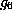 equals its center
and is
equals its center
and is 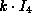 .
.

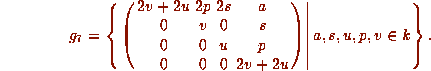 This Lie algebra is solvable.
This Lie algebra is solvable.
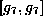 has dimension 2. Its center is 2-dimensional;
its nilpotent radical is 4-dimensional.
has dimension 2. Its center is 2-dimensional;
its nilpotent radical is 4-dimensional.

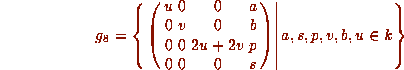 The commutator subalgebra
The commutator subalgebra
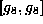 is abelian of dimension 3 and so
is abelian of dimension 3 and so
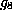 is solvable. Its center is
is solvable. Its center is
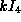 .
Its nilpotent radical is 4-dimensional.
.
Its nilpotent radical is 4-dimensional.

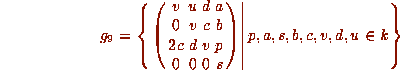 This Lie algebra is solvable.
Its nilpotent radical is 4-dimensional.
Its center is
This Lie algebra is solvable.
Its nilpotent radical is 4-dimensional.
Its center is 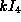 .
.

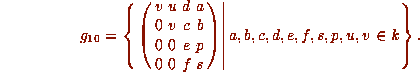 The solvable radical of this Lie algebra is
7-dimensional.
There is a 3-dimensional Levi subalgebra.
The center is
The solvable radical of this Lie algebra is
7-dimensional.
There is a 3-dimensional Levi subalgebra.
The center is 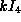 .
.