![[Shownotes]](../gif/annotate/shide-71.gif)
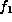 ,
, 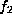 , and
, and
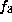 in this paper. However, neither
in this paper. However, neither 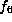 nor its stabilizer is
to be found in [Z], and since [Z] does not give the
full stabilizer of
nor its stabilizer is
to be found in [Z], and since [Z] does not give the
full stabilizer of 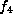 , we present these two as well.
, we present these two as well.
The computation of such a group stabilizer is a less straightforward matter
than the computation of the Lie algebra stabilizer. Our methods are
somewhat
ad hoc, but have in common that they use the Lie algebra in two ways:
both for finding linear tranformations fixing the form f by exponentiating
nilpotent elements of the Lie algebra stabilizer and for finding
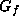 -invariant linear subspaces of
-invariant linear subspaces of 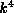 . We use computer algebra packages
such as Mathematica and Maple to check in each case that certain matrices in
. We use computer algebra packages
such as Mathematica and Maple to check in each case that certain matrices in
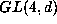 preserve the form. Knowing the dimension of
preserve the form. Knowing the dimension of 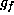 from Table 1
gives a bound for the dimension of the stabilizer. If this is attained by a
subgroup it contains at least the connected component of the full stabilizer
and group arguments involving the normalizer can be used. If not, we use the
packages to show there are no further elements fixing the form.
from Table 1
gives a bound for the dimension of the stabilizer. If this is attained by a
subgroup it contains at least the connected component of the full stabilizer
and group arguments involving the normalizer can be used. If not, we use the
packages to show there are no further elements fixing the form.
The stabilizer of 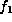 is (as in [Z]) a finite group
isomorphic to
is (as in [Z]) a finite group
isomorphic to 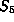 .
It consists of all
.
It consists of all 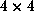 permutation matrices together with all
products PSQ where P and Q are permutation matrices and
S is the matrix
permutation matrices together with all
products PSQ where P and Q are permutation matrices and
S is the matrix

 This is the 4-dimensional constituent of the natural representation
of
This is the 4-dimensional constituent of the natural representation
of 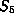 on
on 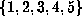 by taking for example the differences of
1 with the remaining integers.
The stabilizer of
by taking for example the differences of
1 with the remaining integers.
The stabilizer of 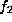 is (as indicated in [Z])
is (as indicated in [Z])

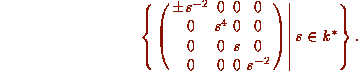

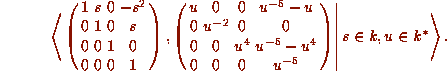

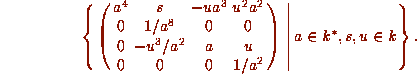

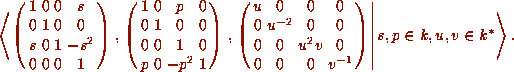 It is straightforward to check that this group fixes
It is straightforward to check that this group fixes 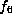 . It has
dimension 4 which is the same as its Lie algebra. By considering
the action on the first, third, and fourth coordinates, it is
immediate that this is
. It has
dimension 4 which is the same as its Lie algebra. By considering
the action on the first, third, and fourth coordinates, it is
immediate that this is 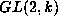 acting faithfully and irreducibly on the
homogeneous degree two polynomials in the two coordinates. It must
then be the connected component of the identity. But this action is
self normalizing in
acting faithfully and irreducibly on the
homogeneous degree two polynomials in the two coordinates. It must
then be the connected component of the identity. But this action is
self normalizing in 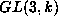 and because it is a direct sum of
a 1-dimensional constituent and this constituent, this is the
full normalizer in
and because it is a direct sum of
a 1-dimensional constituent and this constituent, this is the
full normalizer in 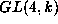 . This establishes this is the
full stabilizer of
. This establishes this is the
full stabilizer of 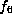 .
.
Note that the forms listed are all distinct. Indeed the dimensions of
the Lie algebras are distinct except for the two of dimension 12 and
the two of dimension 14. The ones of dimension 14, 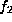 and
and 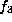 ,
correspond to orbit dimensions 15
and 14 and so are distinct. The Lie algebras for
,
correspond to orbit dimensions 15
and 14 and so are distinct. The Lie algebras for 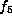 and
and 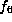 are not isomorphic. Indeed
are not isomorphic. Indeed 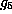 is abelian but
is abelian but 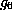 is
not. The forms
is
not. The forms 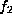 and
and 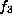 can be also distinguished because the tori
have different eigenvalues. Alternatively, exponentiating a
nilpotent element in the Lie algebra for
can be also distinguished because the tori
have different eigenvalues. Alternatively, exponentiating a
nilpotent element in the Lie algebra for 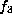 fixes the form but does
not for
fixes the form but does
not for 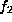 .
.