![[Shownotes]](../gif/annotate/shide-91.gif)
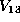 is
equivalent under the
action of
is
equivalent under the
action of 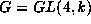 to one of the forms,
to one of the forms, 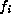 , in Table 1 with
, in Table 1 with
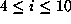 . We do this in a series of lemmas which themselves
provide an algorithm for transforming an arbitrary form in
. We do this in a series of lemmas which themselves
provide an algorithm for transforming an arbitrary form in 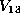 into
the appropriate
into
the appropriate 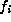 .
.

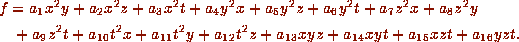 Our goal is to study the orbits under G of
f. To this end, we may (and frequently shall)
freely replace f by its image under an element
Our goal is to study the orbits under G of
f. To this end, we may (and frequently shall)
freely replace f by its image under an element
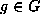 .
.
Lemma. Each nonzero form is equivalent to a form as in Case 1 or Case 2:

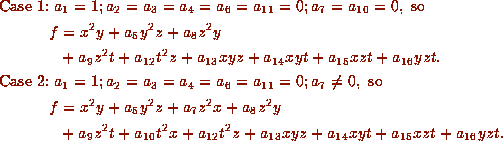
Without loss of generality, we may assume that a term not involving
z is nonzero. We may then use the above Proposition 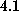 on the
variables x,y, and t so that the terms in the form f involving
only these add up to
on the
variables x,y, and t so that the terms in the form f involving
only these add up to 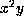 ,
, 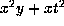 , or xyt. If it is xyt
replace t by t+x to get
, or xyt. If it is xyt
replace t by t+x to get 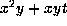 . This means we can assume
. This means we can assume


Several times during the paper we
will transform by a diagonal matrix in G which amounts to transforming
each of x,y,z,t by various scalars. We refer to this as scaling.
In doing so, we will always without
reference be sure that the coefficients which have been fixed are
not changed.
Now scale to get 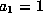 (e.g., use the diagonal
matrix
(e.g., use the diagonal
matrix 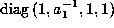 ).
).
In the sequel we
will denote transformations under G
by indicating the replacements to be performed. In particular, the
substitution of y by 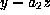 will be given by
will be given by
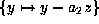 . Do this substitution
to obtain a new form in which
. Do this substitution
to obtain a new form in which
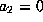 as well. The terms which were
assumed to be 0 are still 0;
the coefficients
as well. The terms which were
assumed to be 0 are still 0;
the coefficients 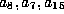 , and
, and
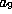 may have changed, the remaining terms have not.
may have changed, the remaining terms have not.
If we are not yet in Case 1 or 2, we must have 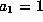 ,
, 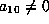 ,
and
,
and 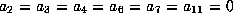 .
Now scale to get
.
Now scale to get 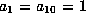 (e.g., by
(e.g., by 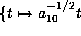 ).
Next apply
).
Next apply 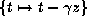 to obtain a new form in which the terms
that were assumed to be zero remain zero, except for
to obtain a new form in which the terms
that were assumed to be zero remain zero, except for
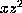 whose coefficient becomes
whose coefficient becomes 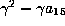 . Choose
. Choose 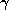 so that this is not 0 and the form is as in Case 2.
so that this is not 0 and the form is as in Case 2.
A form f is in 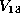 if all
if all 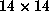 submatrices of
submatrices of 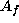 have determinant 0. If some
have determinant 0. If some 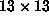 submatrix is nonsingular,
then f is not in
submatrix is nonsingular,
then f is not in 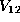 . The method will be to take a form as
described above and find suitable
. The method will be to take a form as
described above and find suitable 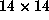 submatrices for which
the determinant 0 condition forces conditions on the coefficients.
submatrices for which
the determinant 0 condition forces conditions on the coefficients.
For subsets J,K of 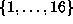 of equal size,
we denote by
of equal size,
we denote by 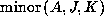 the determinant of the
submatrix of a square matrix A
obtained by excluding the rows J and
columns K. For example, the submatrix excluding rows 2,3
and columns 5,6 would have determinant denoted by
the determinant of the
submatrix of a square matrix A
obtained by excluding the rows J and
columns K. For example, the submatrix excluding rows 2,3
and columns 5,6 would have determinant denoted by

 If f is in
If f is in 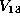 , then
, then
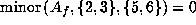 . It is this kind of
equation
that we shall use throughout to find restrictions on the coefficients
. It is this kind of
equation
that we shall use throughout to find restrictions on the coefficients 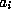 .
We shall divide the work according to the two cases found in Lemma 5.1.
.
We shall divide the work according to the two cases found in Lemma 5.1.
Case 1.
We take a form as described above in Case 1.
We have 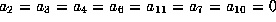 . We wish to
show
. We wish to
show 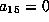 and so assume it is not.
However,
in order to do part of Case 2 we also must release
and so assume it is not.
However,
in order to do part of Case 2 we also must release 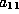 and
and
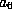 meaning they are not necessarily 0.
meaning they are not necessarily 0.
Lemma. If f satisfies

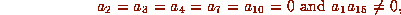 then Gf contains a form
then Gf contains a form 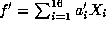 with
with

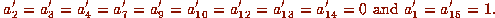
We can scale z (i.e., multiply z by the scalar 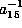 ,
fixing the remaining variables),
so that the resulting coefficient
,
fixing the remaining variables),
so that the resulting coefficient 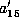 is 1. The coefficient
is 1. The coefficient
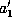 of
of 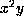 remains 1. We assume then that
remains 1. We assume then that 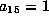 .
.
Perform the substitution
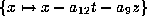 to get a form in which
to get a form in which
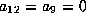 . No new terms appear and
. No new terms appear and 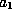 and
and 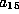 are still
1.
are still
1.
Finally do the transformation
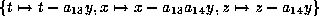 .
This sets
.
This sets 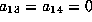 , adds no new terms and keeps the
nonzero terms as they were. When we transform this way,
we have always checked
that the transformation is invertible.
, adds no new terms and keeps the
nonzero terms as they were. When we transform this way,
we have always checked
that the transformation is invertible.
Lemma.
Let 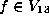 be as
be as 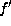 in the previous lemma
and assume
in the previous lemma
and assume 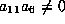 .
Then Gf contains
.
Then Gf contains 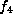 .
.
Set 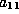 equal to 1 by
scaling
equal to 1 by
scaling
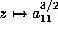 ,
, 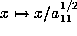 ,
,
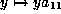 ,
, 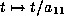 .
Also,
by scaling
.
Also,
by scaling
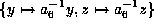 and multiplying by
and multiplying by 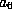 we can
assume
we can
assume 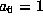 as well.
as well.
Now
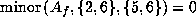 gives
gives 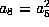 and
and
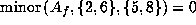 gives
gives 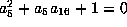 .
In particular,
.
In particular, 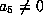 .
Now factor
.
Now factor
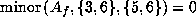 to get
to get 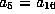 .
The previous equation for
.
The previous equation for 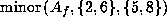 gives
gives 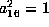 and so
and so 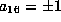 . If
. If
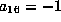 , the transform
, the transform
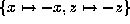 leads to
leads to

 which is the case
which is the case 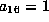 .
Thus, we may assume
.
Thus, we may assume 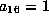 .
But now the transformation
.
But now the transformation
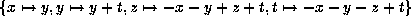 gives the
form
gives the
form 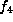 .
.
A word is in order here about how such tranformations are found.
For a given form f, its Lie algebra stabilizer 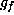 can
be found as described in .1.
The Lie algebra for the form above consists of a 3-dimensional
commutative Lie algebra of linear tranformations all of which
have a unique eigenvector. The same is true of the Lie algebra of
the form
can
be found as described in .1.
The Lie algebra for the form above consists of a 3-dimensional
commutative Lie algebra of linear tranformations all of which
have a unique eigenvector. The same is true of the Lie algebra of
the form 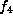 in Table 1. The transformation above is found by
producing an element of G which under conjugation transforms
one Lie algebra to the other.
Lemma.
Let
in Table 1. The transformation above is found by
producing an element of G which under conjugation transforms
one Lie algebra to the other.
Lemma.
Let 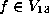 be as
be as 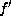 in Lemma 5.2
and assume
in Lemma 5.2
and assume 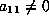 ,
, 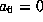 .
Then Gf contains
.
Then Gf contains 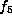 .
.
As in the first paragraph of the proof of the previous lemma, we can
set 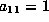 .
Now
.
Now
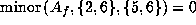 gives
gives 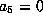 .
Next,
.
Next,
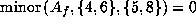 gives
gives 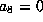 or
or
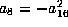 .
.
Here
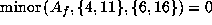 gives
gives
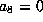 or
or 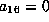 and so
and so 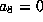 .
Now
.
Now
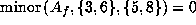 gives
gives 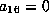 .
Thus, the form is
.
Thus, the form is

 Finally, transform this form according to
Finally, transform this form according to
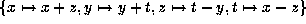 .
This gives
.
This gives 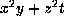 , that is,
, that is, 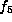 .
.
We may now assume that 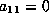 . We are still assuming as well that
. We are still assuming as well that
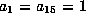 and
and 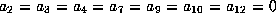 .
.
Lemma.
Suppose that 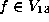 is as
is as 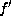 in Lemma 5.2.
If
in Lemma 5.2.
If 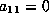 ,
then f is equivalent to one of
,
then f is equivalent to one of 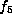 ,
, 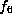 or
or 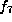 .
.
The equations 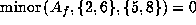 and
and
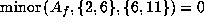 give
give
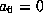 and
and
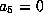 , respectively.
, respectively.
But
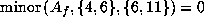 gives
gives 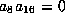 , so at least one of
, so at least one of
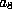 ,
, 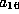 must be 0. The form is now
must be 0. The form is now

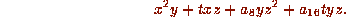
If 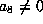 , scale by
, scale by 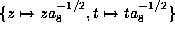 to get
to get
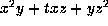 ;
after interchanging
t and z this gives
;
after interchanging
t and z this gives
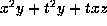 , which was shown to be equivalent to
, which was shown to be equivalent to
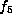 in the proof of Lemma 5.4.
in the proof of Lemma 5.4.
If 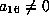 scale x and t by
scale x and t by 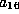 to get
to get 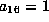 and the form is
and the form is 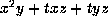 which modulo cubics is
which modulo cubics is
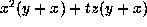 which is equivalent to
which is equivalent to 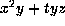 .
This is
.
This is 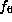 .
.
Finally, if both 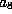 and
and 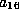 are 0, it is
are 0, it is 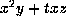 which becomes
equal to
which becomes
equal to 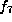 by interchanging y and t.
by interchanging y and t.
These lemmas show that any form which satisfies the conditions of Lemma 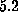 is listed in the table. We can go back
to the beginning of Case 1 and assume
is listed in the table. We can go back
to the beginning of Case 1 and assume 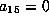 . We assume that
. We assume that 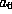 and
and 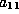 are 0 as our only need in Case 2 will
be when
are 0 as our only need in Case 2 will
be when 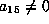 .
.
Lemma.
Assume f is a form satisfying
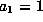 and
and 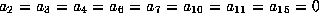 .
Then f is equivalent to a form
.
Then f is equivalent to a form 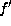 with
with
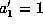 and
and 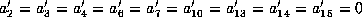 .
.
Apply 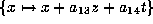 to get
to get 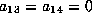 . Notice
. Notice
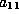 which had been 0 may now be nonzero.
which had been 0 may now be nonzero.
Lemma.
Assume 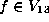 is as in
is as in 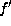 in Lemma 5.6.
If
in Lemma 5.6.
If 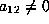 ,
then f is equivalent to
,
then f is equivalent to 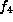 or
or 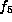 .
.
Set 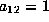 and then
and then 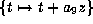 gives
gives 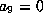 .
Now
.
Now 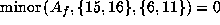 gives
gives 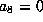 . Again
. Again
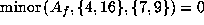 gives
gives
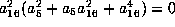 . This means that
. This means that
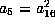 or
or 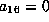 .
.
Suppose first that 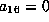 . Then
. Then 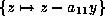 gives
gives 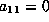 and
the form is
and
the form is 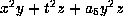 . If
. If 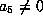 , this can be
scaled to
, this can be
scaled to 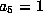 .
This, however, has rank 14 and so is not in
.
This, however, has rank 14 and so is not in 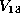 . It is easily seen to
be equivalent to
. It is easily seen to
be equivalent to 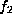 by the cyclic permutation
by the cyclic permutation 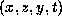 .
Otherwise,
.
Otherwise, 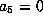 and the form is
and the form is 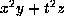 which
is
which
is 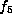 after interchanging t and z.
after interchanging t and z.
We can then assume 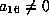 and
and 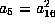 . The form is now
. The form is now

 Scale by
Scale by 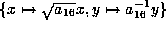 to
get
to
get 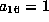 . Now apply
. Now apply 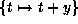 to get the form
to get the form
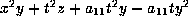 . If
. If 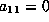 , the form is
, the form is 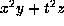 which has rank 12 and is equivalent to
which has rank 12 and is equivalent to 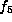 after interchanging t and
z. If not, scale by
after interchanging t and
z. If not, scale by 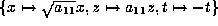 to get
to get
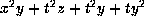 . Now apply
. Now apply 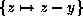 and
then again
and
then again 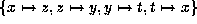 to get
to get 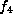 .
Lemma.
Assume
.
Lemma.
Assume 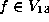 is as
is as 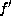 in Lemma 5.6.
in Lemma 5.6.
If 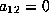 and
and 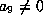 ,
then f is equivalent to
,
then f is equivalent to 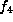 or to
or to 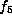 .
.
The equation 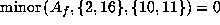 gives
gives 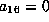 .
Now
.
Now 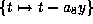 gives
gives 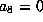 . If
. If 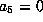 , this is
, this is 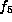 . If not
scale to get
. If not
scale to get 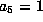 . This is
. This is 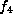 after interchanging x with z and t
with y.
after interchanging x with z and t
with y.
To finish Case 1,
it remains to consider f as 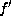 in Lemma 5.6 with
in Lemma 5.6 with 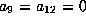 .
Lemma.
Assume f is as
.
Lemma.
Assume f is as 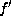 in Lemma 5.6.
If
in Lemma 5.6.
If 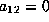 and
and 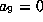 ,
then f is equivalent to one of
,
then f is equivalent to one of 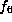 ,
, 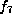 ,
,
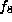 ,
, 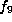 ,
, 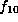 .
.
First, assume 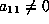 . The substitution
. The substitution
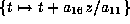 gives
gives 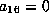 .
Scale to get
.
Scale to get 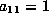 .
.
If 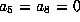 , then f is a form in 3 variables, and hence known
by Propositon 4.1 to be equivalent to one of
, then f is a form in 3 variables, and hence known
by Propositon 4.1 to be equivalent to one of 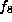 ,
, 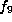 ,
, 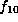 .
.
If both 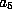 and
and 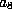 are nonzero, scale by
are nonzero, scale by

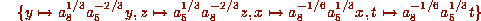 to get
to get
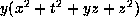 .
Now apply
.
Now apply 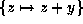 to get
the form
to get
the form 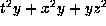 which has rank 12.
It can be factored as
which has rank 12.
It can be factored as 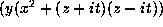 where i is the square
root of -1. The transform
where i is the square
root of -1. The transform 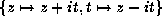 then yields
then yields
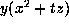 , the form
, the form 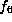 on the list.
on the list.
If 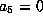 and
and 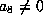 , then the form is
, then the form is
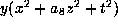 , which is readily seen to be
equivalent to
, which is readily seen to be
equivalent to 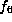 again.
again.
If 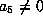 and
and 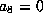 , then the form is
, then the form is
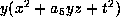 . Scaling to
. Scaling to 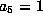 and transforming via
and transforming via 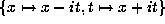 , gives
, gives 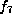 after a permutation of variables.
after a permutation of variables.
It remains to consider the case 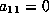 .
The form is now
.
The form is now

 If
If 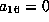 , this is in 3 variables and we are done by Proposition 4.1.
If not scale to get
, this is in 3 variables and we are done by Proposition 4.1.
If not scale to get 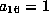 . Then
. Then
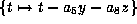 gives
gives 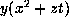 which is
which is 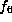 .
.
This completes Case 1.
Case 2.
In this case we assume 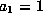 ,
, 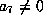 and
and 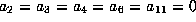 .
.
Lemma.
Assume f satisfies 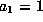 ,
, 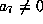 and
and
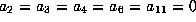 .
Then f is equivalent to a form
.
Then f is equivalent to a form 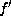 with
with
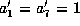 and
and
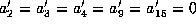 .
.
First of all, we can set 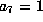 by scaling. Apply
by scaling. Apply
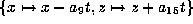 to make
to make 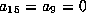 ; this
keeps
; this
keeps 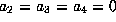 , but releases
, but releases
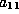 and
and 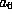 .
.
Lemma.
Suppose f is as 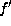 in Lemma 5.10.
If
in Lemma 5.10.
If 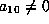 ,
then f is equivalent to a form as in Lemma 5.2; in particular,
Gf contains a form in Case 1.
,
then f is equivalent to a form as in Lemma 5.2; in particular,
Gf contains a form in Case 1.
By scaling set 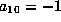 .
Now make the transform
.
Now make the transform 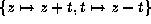 .
This gives a form in which
.
This gives a form in which 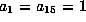 and
and
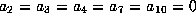 , that is, as required.
, that is, as required.
We may assume then
that 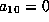 .
At various stages during this case we will make the following
substitution, where
.
At various stages during this case we will make the following
substitution, where 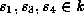 ,
,

 It leaves the fixed coefficients the same
with the exception of
It leaves the fixed coefficients the same
with the exception of 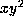 which has coefficient
which has coefficient
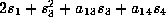 . The coefficients of
xyz, yzt, and
. The coefficients of
xyz, yzt, and 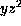 have become
have become 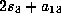 ,
,
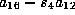 and
and 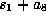 ,
respectively. We will make choices of the
,
respectively. We will make choices of the 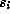 in such a way
that the coefficient
in such a way
that the coefficient 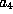 of
of 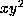 remains 0 and some of the
other coefficients become 0.
Lemma.
Suppose f is as
remains 0 and some of the
other coefficients become 0.
Lemma.
Suppose f is as 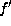 in Lemma 5.10 with
in Lemma 5.10 with 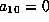 and
and
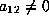 . If
. If 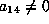 ,
then f is equivalent to such a form
,
then f is equivalent to such a form 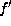 with
with 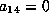 .
.
By scaling, set 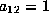 . The fact that
. The fact that 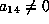 means we
can choose
means we
can choose 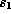 and
and 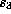 as we wish and then choose
as we wish and then choose 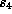 so that
after transforming by
so that
after transforming by 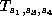 ,
the coefficient of
,
the coefficient of 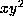 is 0. By choosing
is 0. By choosing 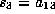 and
and 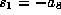 and
and
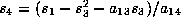 , we can apply
, we can apply
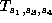 to obtain a form in which
to obtain a form in which 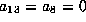 .
Now substitute
.
Now substitute 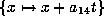 and then
and then 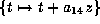 . This
gives a form with
. This
gives a form with 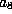 released but no other new nonzero
terms and
released but no other new nonzero
terms and 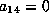 .
We could
proceed with this value for
.
We could
proceed with this value for 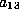 but we will need to
do the case without this restriction anyway which we do below.
but we will need to
do the case without this restriction anyway which we do below.
Lemma.
Suppose 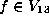 is as in Lemma 5.10.
If
is as in Lemma 5.10.
If 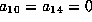 and
and 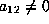 ,
then f is equivalent to
,
then f is equivalent to 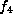 .
.
By scaling set 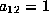 . Pick
. Pick 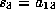 and
and
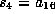 and apply
and apply 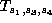 to get a form in which
to get a form in which 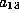 and
and 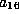 are 0. We must then choose
are 0. We must then choose 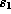 so that the coefficient of
so that the coefficient of
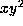 is 0 which we may do.
is 0 which we may do.
Now
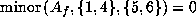 gives
gives
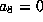 and
and
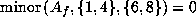 gives
gives
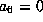 .
Moreover,
.
Moreover, 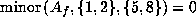 gives
gives 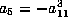 . Now,
application of
. Now,
application of 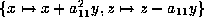 and then
and then
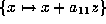 gives
gives 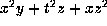 .
After interchanging z and t, this becomes
.
After interchanging z and t, this becomes 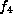 of Table 1.
of Table 1.
Lemma.
Suppose 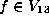 is as
is as 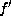 in Lemma 5.10.
If
in Lemma 5.10.
If 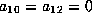 then f is equivalent to a form in Case 1 or a form in three variables.
then f is equivalent to a form in Case 1 or a form in three variables.
Again we distinguish between whether or not
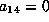 . Suppose it is not and set it to 1. As
above we can make substitutions
. Suppose it is not and set it to 1. As
above we can make substitutions
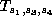 with
with 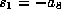 ,
, 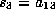 and
and 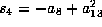 to make
to make 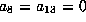 . Now let
. Now let
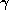 be a cube root of
be a cube root of 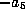 . Then transform by
. Then transform by
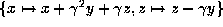 . This gives
. This gives
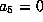 as well. But then, transforming by
as well. But then, transforming by 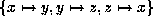 gives a form in Case 1.
We can now
assume that
gives a form in Case 1.
We can now
assume that 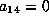 .
For the last time transform with
.
For the last time transform with 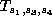 for
appropriately chosen
for
appropriately chosen 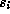 . As before
we can choose
. As before
we can choose 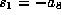 to make
to make
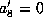 . We choose
. We choose 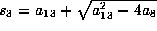 ,
so that the coefficient
,
so that the coefficient 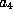 of
of
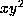 remains 0.
remains 0.
The transformed coefficient
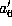 of
of
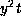 is
is 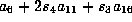 .
If
.
If 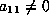 we can choose
we can choose 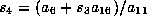 so that
so that
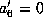 and
and 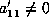 .
.
Then
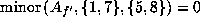 gives the contradiction
gives the contradiction
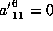 .
.
This means we can assume 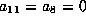 but
but
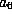 is no longer restricted to 0.
Now
is no longer restricted to 0.
Now
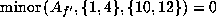 gives
gives 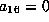 . If
. If
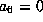 , the form is in 3 variables and we are done.
, the form is in 3 variables and we are done.
Assume not; we can then scale to 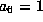 .
Now apply
.
Now apply 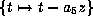 to get
to get
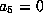 . The form is now
. The form is now

 Again set
Again set 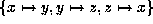 to get
to get

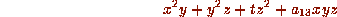 which is a form as in Case 1.
which is a form as in Case 1.
This finishes Case 2 completely.
Thus, we have shown that all forms in 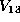 are
as listed in Table 1.
are
as listed in Table 1.