Contents Next: Dougall's Theorem. Up: Pfaff's Method (III): Comparison Previous: Pfaff's Theorem.

Bailey's Theorem.

The result in question [5, p. 512, eq.(c),] is

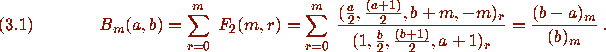
The two methods now diverge completely. The WZ method produces a second order recurrence for 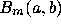, namely

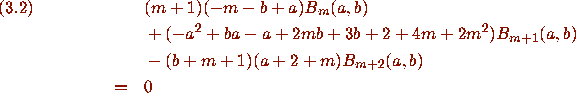and proves it by showing that if

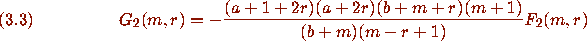then

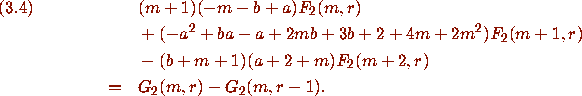
Identity (3.2) then follows by summing (3.4) from r=0 to r=m+2 (i.e. Zeilberger's creative telescoping [15].

This, of course provides a perfectly valid proof of (3.1); however we note the inability of the WZ method to establish directly

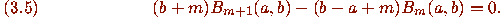The Pfaff method, on the other hand, cannot handle (3.1) by itself. It must simultaneously prove that [3, p. 2, eq.(2.3),]

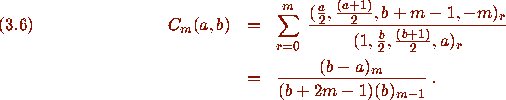Pfaff's method proceeds now as in Section 2. Here we find directly [2, ,]

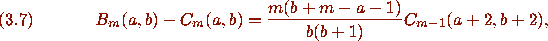and

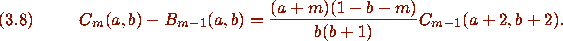Pfaff's method then concludes by the observation that the right-hand sides of (3.1) and (3.6) also satisfy (3.7) and (3.8). Thus Pfaff's method requires two first order recurrences based on two conjectured summation identities (i.e. (3.1) and (3.6)). In some sense, both methods work twice as hard as in Section 2; however, Pfaff's method proves twice as much for twice as much work.

Contents Next: Dougall's Theorem. Up: Pfaff's Method (III): Comparison Previous: Pfaff's Theorem.