![[Shownotes]](../gif/annotate/shide-51.gif)
In the first paper in this series [1], we used Pfaff's method to prove that

 where
where

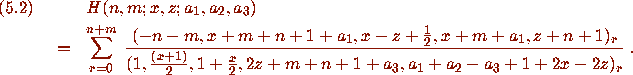 The proof resembled the Pfaff method proofs already examined in this
paper. The only difference was that it was necessary to prove
twenty identities simultaneously of which (5.1) was just one. Thus,
in addition to (5.1), we also proved, for example,
The proof resembled the Pfaff method proofs already examined in this
paper. The only difference was that it was necessary to prove
twenty identities simultaneously of which (5.1) was just one. Thus,
in addition to (5.1), we also proved, for example,



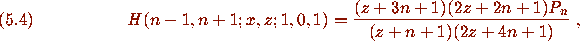

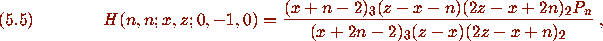 plus sixteen similar results; here
plus sixteen similar results; here

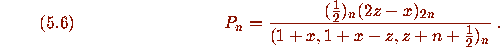
For example [1, eq.(5.12),]

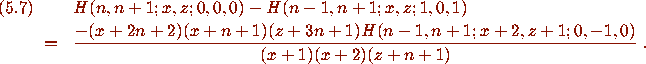
To summarize, the Pfaff method is cumbersome for this problem. No single step is substantially more difficult than the steps in Pfaff's own work (i.e. Section 2). However, the proof of twenty theorems simultaneously requires a good deal more than twenty times the effort required in Section 2. First the twenty results like (5.1) and (5.3)--(5.5) must be found empirically. Then twenty recurrences must be selected from a multitude in order to prove all twenty results.
In contrast, the application of the WZ method to prove (5.1) and (5.5) is ongoing. The question of whether WZ could prove (5.1) was raised at the Ann Arbor Conference on Combinatorics in June, 1994. Theoretically there is no doubt that the WZ method can produce a proof of both (5.1) and (5.5) eventually. After the conference, Zeilberger developed a modification of the WZ method designed to exploit the shifts of parameters that are so effective in the Pfaff approach.
The following is a summary of accomplishment of the WZ method in treating (5.1) and (5.5).
First we let

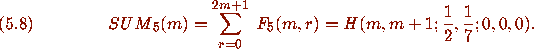 Then SUM
Then SUM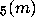 satisfies the following linear recurrence equation
(graciously supplied by Zeilberger)
satisfies the following linear recurrence equation
(graciously supplied by Zeilberger)

 This is proved by constructing a gigantic certificate function
This is proved by constructing a gigantic certificate function

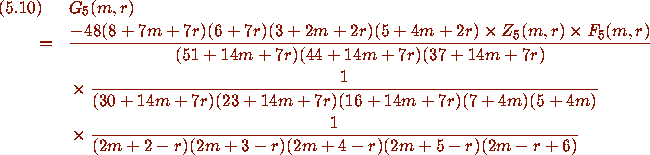 where
where

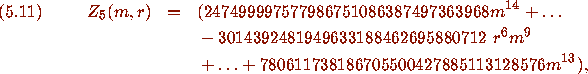 a polynomial of 180 terms with coefficients often in the nonillions
or decillions.
a polynomial of 180 terms with coefficients often in the nonillions
or decillions.
Zeilberger discovered that the shifts 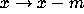 ,
, 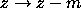 greatly
improve the effectiveness of the WZ-method. He was then able to
obtain the following results for
greatly
improve the effectiveness of the WZ-method. He was then able to
obtain the following results for

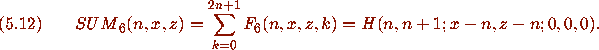 Then SUM
Then SUM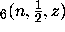 satisfies
satisfies

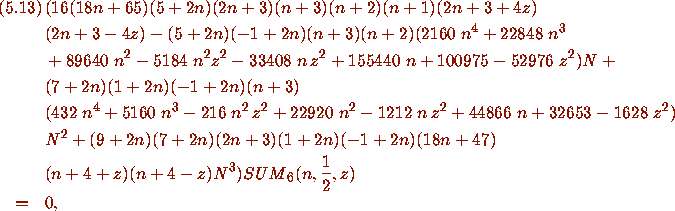 where
where 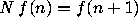 .
The related certificate function is
.
The related certificate function is

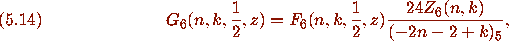 with
with

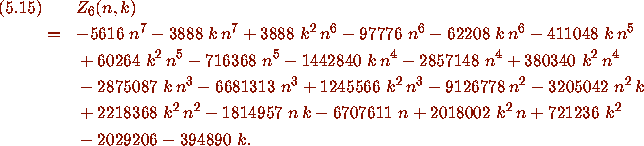
Using his shift modification of the WZ method, Zeilberger has found a
recurrence for the full 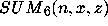 thus giving a new proof of (5.1), and recently Peter Paule has
obtained the relevant certificate without
the shift modification.
Both the recurrence and the certificate function are too long to be
included here. Suffice it to say that the large polynomial (analogous
to (5.11)) in n,k,x and z arising in Zeilberger's
certificate function has
944 terms by my count and occupies twelve pages of printout.
At this moment, (5.5) has still not yielded to the WZ method or its
modifications. However it is surely only a matter of time before
improvements in MAPLE combined with larger machines will produce a
recurrence satisfied by (5.5).
thus giving a new proof of (5.1), and recently Peter Paule has
obtained the relevant certificate without
the shift modification.
Both the recurrence and the certificate function are too long to be
included here. Suffice it to say that the large polynomial (analogous
to (5.11)) in n,k,x and z arising in Zeilberger's
certificate function has
944 terms by my count and occupies twelve pages of printout.
At this moment, (5.5) has still not yielded to the WZ method or its
modifications. However it is surely only a matter of time before
improvements in MAPLE combined with larger machines will produce a
recurrence satisfied by (5.5).
Suppose that we actually had in hand the mega-massive general certificate function. We would then have a proof of (5.5) with little insight gained and by means of a recurrence so huge that no hand calculation could check it.
In contrast, Pfaff's method actually succeeds in proving (5.1) and
(5.5) plus eighteen other identities. The proof is checkable by hand
at each step. Also we learn that there is a cluster of identities
(the computer suggests more than fifty, see [1, Section 6,])
intimately tied up with
(5.1); each of these other identities conveys more information about
its structure than (5.1) because (5.1) is the only one for which the
right hand side is identically zero.