![[Shownotes]](../gif/annotate/sshow-71.gif)
Given the contest atmosphere created by Sections 5 and 6, it seems appropriate to devote some time to the countless instances wherein the WZ-method succeeds completely and Pfaff's method falls on its face.
The WZ method has successfully found a recurrence for the 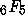 appearing in (8.1) of [2]. This identity was posed as a conjecture
at the Ann Arbor Conference on Algebra and Combinatorics in June
1994. D. Stanton observed that it is a special case of [8, eq. (1.8),]
(Click here to see this equation)
and subsequently D. Zeilberger proved it by using the WZ method to
find a recurrence. A fuller account will appear elsewhere [4].
In addition, I have been unable to prove any ``series to series''
identities using Pfaff. Perhaps Whipple's celebrated theorem [12]
(cf. [6, p. 25, eq. (4),]) will be the most instructive example.
appearing in (8.1) of [2]. This identity was posed as a conjecture
at the Ann Arbor Conference on Algebra and Combinatorics in June
1994. D. Stanton observed that it is a special case of [8, eq. (1.8),]
(Click here to see this equation)
and subsequently D. Zeilberger proved it by using the WZ method to
find a recurrence. A fuller account will appear elsewhere [4].
In addition, I have been unable to prove any ``series to series''
identities using Pfaff. Perhaps Whipple's celebrated theorem [12]
(cf. [6, p. 25, eq. (4),]) will be the most instructive example.

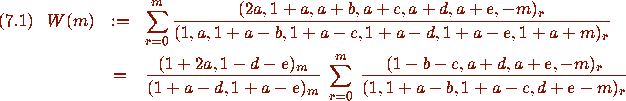 The left-hand side of (7.1) is one parameter freer than the series in
(4.1) and consequently any generalization of the recurrences in
Section 4 would presumably involve a shift of a to a+1 with
b,c,d and e unaltered.
The left-hand side of (7.1) is one parameter freer than the series in
(4.1) and consequently any generalization of the recurrences in
Section 4 would presumably involve a shift of a to a+1 with
b,c,d and e unaltered.
On the other hand the right-hand side of (7.1) is a balanced series and is thus
amenable to Pfaff's method as outlined in [1, Section 2,] (see also
Sections 2 and 3 of this paper). This approach would yield shifts of
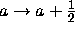
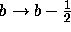 ,
, 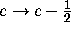 ,
, 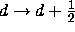 ,
, 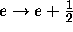 .
.
As a result there is no obvious, simple way of reconciling the resulting first order recurrences because of the varying parameter shifts.
In contrast, the WZ method smoothly nails Whipple's theorem by showing that each side of (7.1) satisfies the second order recurrence

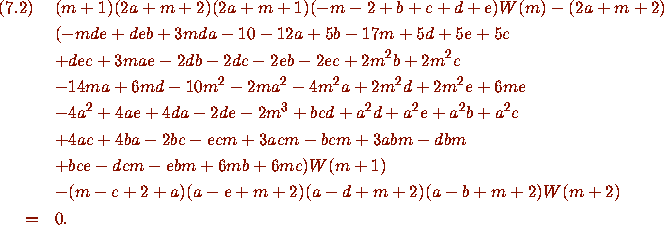
The wide applicability of the WZ method [7], [13], [15], [16], [17] and its beautiful automation by Zeilberger [14] make it a method that will have a permanent place in the theory of hypergeometric series. Certainly Pfaff's method as currently understood is no match for it in general.