

Contents
Next: The PSLQ Integer
Up: Recognizing Numerical
Previous: Abstract
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-21.gif)
1. Introduction
The advent of inexpensive, high-performance computers and new
efficient algorithms have made possible the automatic recognition of
numerically computed constants. In other words, techniques now exist
for determining, within certain limits, whether a computed real or
complex number can be written as a simple expression involving the
classical constants of mathematics.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-22.gif)
The fundamental technique involved is that of finding integer
relations. Let 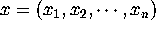 be a vector of real
numbers. x is said to possess an integer relation if there exist
integers
be a vector of real
numbers. x is said to possess an integer relation if there exist
integers 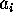 not all zero such that
not all zero such that 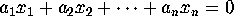 . By an integer relation algorithm, we mean an algorithm
that is guaranteed (provided the computer implementation has
sufficient numeric precision) to recover the vector of integers
. By an integer relation algorithm, we mean an algorithm
that is guaranteed (provided the computer implementation has
sufficient numeric precision) to recover the vector of integers 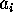 ,
if it exists, or to produce bounds within which no integer relation
can exist.
,
if it exists, or to produce bounds within which no integer relation
can exist.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-23.gif)
The problem of finding integer relations among a set of real numbers
was first studied by Euclid, who gave an iterative algorithm (the
Euclidean algorithm), which when applied to two real numbers, either
terminates, yielding an exact relation, or produces an infinite
sequence of approximate relations. The generalization of this problem
for n > 2 has been attempted by Euler, Jacobi, Poincare, Minkowski,
Perron, Brun, Bernstein, among others. However, none of their
algorithms has been proven to work for n > 3, and numerous
counterexamples have been found.
The first integer relation algorithm with the desired properties
mentioned above was discovered by Ferguson and Forcade in 1977
[14]. In the intervening years a number of other integer
relation algorithms have been discovered, including the ``LLL''
algorithm [16], the ``HJLS'' algorithm [15], and the
``PSOS'' [6] algorithm.
![[Shownotes]](../gif/annotate/sshow-21.gif)
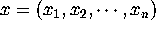 be a vector of real
numbers. x is said to possess an integer relation if there exist
integers
be a vector of real
numbers. x is said to possess an integer relation if there exist
integers 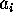 not all zero such that
not all zero such that 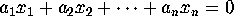 . By an integer relation algorithm, we mean an algorithm
that is guaranteed (provided the computer implementation has
sufficient numeric precision) to recover the vector of integers
. By an integer relation algorithm, we mean an algorithm
that is guaranteed (provided the computer implementation has
sufficient numeric precision) to recover the vector of integers 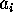 ,
if it exists, or to produce bounds within which no integer relation
can exist.
,
if it exists, or to produce bounds within which no integer relation
can exist.