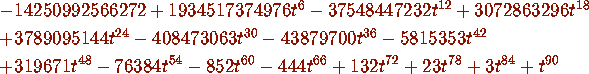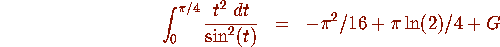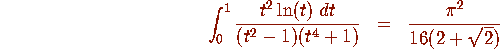Contents
Next: References
Up: Recognizing Numerical
Previous: New Formulas for
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-81.gif)
8. A General Constant Recognition Procedure
In all of the cases mentioned above, the authors of the respective
studies had ``hunches'' beforehand as to what form the resulting
formulas might take. Frankly, some insight of sort is invaluable in
avoiding what otherwise is an exponential explosion in the number of
possible terms. It simply is not possible to perform integer relation
searches with every conceivable term. In fact, if the constant is
known to only limited precision, the number of terms that can be
considered in an integer relation search may be limited to a handful.
Nonetheless, it does appear feasible to define procedures that are
successful in recovering the analytic form of many constants that
naturally appear in mathematical calculations. The authors present
the following procedure as an example:
- Using PSLQ and full precision, check if
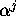 is algebraic
of degree n, for j up to m.
is algebraic
of degree n, for j up to m.
- Using PSLQ and full precision, check if
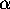 is given by a
multiplicative formula of the form
is given by a
multiplicative formula of the form

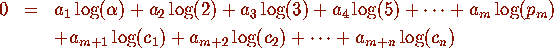
where  is the k-th prime, and where
is the k-th prime, and where  are a selected set of
transcendentals.
are a selected set of
transcendentals.
- Using PSLQ and quad precision, check if
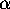 is given by a
linear formula of the form
is given by a
linear formula of the form

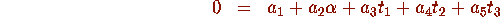
where 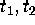 and
and 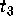 are each a product of up to three constants
from a set of algebraic and/or transcendental constants.
are each a product of up to three constants
from a set of algebraic and/or transcendental constants.
- If a tentative relation is found in the previous step using quad
precision, then check it using full precision.
Some examples of constants recognized by above procedure are the
following:
- The root near 1.3851367 of the polynomial

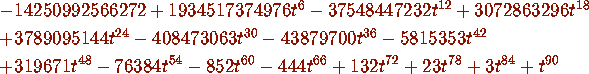
- The definite integral


- The definite intregral

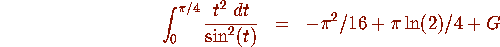
- The definite integral

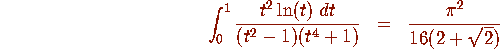
![[Shownotes]](../gif/annotate/sshow-81.gif)
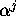 is algebraic
of degree n, for j up to m.
is algebraic
of degree n, for j up to m.
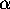 is given by a
multiplicative formula of the form
is given by a
multiplicative formula of the form

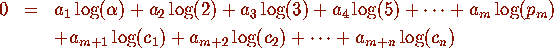
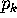 is the k-th prime, and where
is the k-th prime, and where 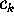 are a selected set of
transcendentals.
are a selected set of
transcendentals.
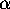 is given by a
linear formula of the form
is given by a
linear formula of the form

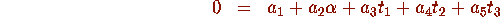
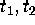 and
and 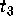 are each a product of up to three constants
from a set of algebraic and/or transcendental constants.
are each a product of up to three constants
from a set of algebraic and/or transcendental constants.