![[Shownotes]](../gif/annotate/shide-11.gif)
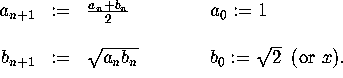

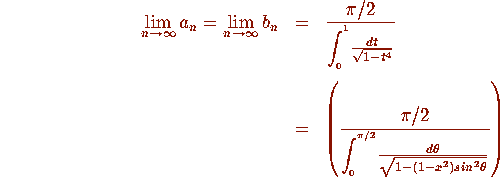 In 1799, Gauss observed this purely numerically and wrote
that this result
In 1799, Gauss observed this purely numerically and wrote
that this result Equivalent Modular Parameterization
This is equivalent to the identities

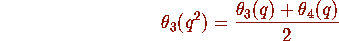 and
and

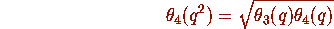 where
where
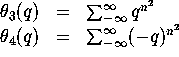
These are modular forms. So for example

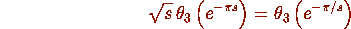
A Cubic Analogue of the AGM
Let

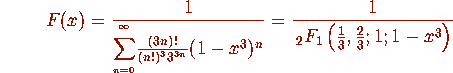
The convergence is cubic.
Proof: The proof is opaque. It works because 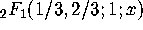 satisfies
satisfies

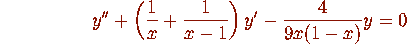


In the above notation.

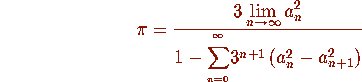 where
where 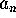 is, as above, with,
is, as above, with, 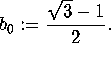 Taking k+1 terms of the sum and limit gives a cubically convergent
algorithm. Twenty one terms gives three billion
digits.The underlying cubic transformation is beautiful:
Taking k+1 terms of the sum and limit gives a cubically convergent
algorithm. Twenty one terms gives three billion
digits.The underlying cubic transformation is beautiful:



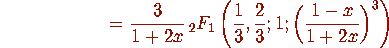
Equivalent Modular Parameterization If

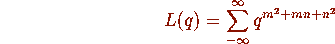 and
and

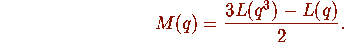 Then
Then

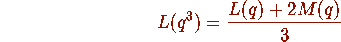 and
and

 Note that if
Note that if 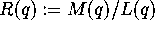 then
then

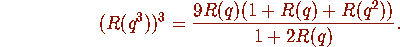 This is a cubic modular equation for R.
This is a cubic modular equation for R.
See Some cubic modular identities of Ramanujan by J. Borwein, P. Borwein & F. Garvan in Trans. A.M.S. 343 (1994) 35-47.
Some Explanations

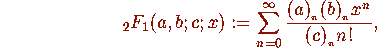 where
where 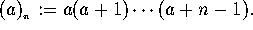
Let

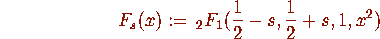

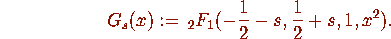
Then

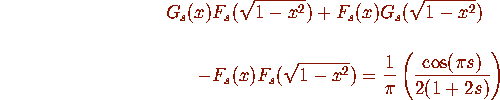 and
and

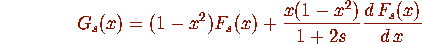

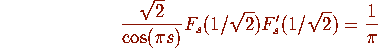
If we can compute 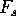 iteratively we can compute
iteratively we can compute 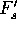 and
and 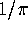 by a second
linked iteration.
by a second
linked iteration.
There are four particularly interesting cases.

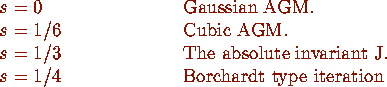
Inverting the ratios
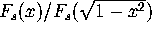 gives elliptic modular functions. Which reduces much of
this to an algebraic theory.
gives elliptic modular functions. Which reduces much of
this to an algebraic theory.
Finding and proving these iterations can (at least in principal) be effected entirely computationally.
The Quadratic s=1/4 Iteration
Let and
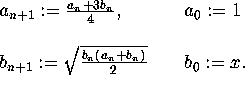 Then the common limit is
Then the common limit is

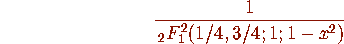 Caveat Emptor: Let
and
Caveat Emptor: Let
and
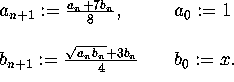 Then the common limit
Then the common limit 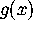 is not differentially algebraic.
is not differentially algebraic.