A Salem number 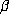 of degree 6 has a minimal polynomial of the following form:
of degree 6 has a minimal polynomial of the following form:

 where a,b and c are integers. The trace of
where a,b and c are integers. The trace of 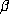 is
is
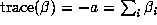 , where the sum is over the six conjugates
of
, where the sum is over the six conjugates
of 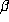 , i.e., the six roots of (2.1). Two of these conjugates are
, i.e., the six roots of (2.1). Two of these conjugates are 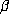 and
and
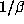 and the remaining conjugates satisfy
and the remaining conjugates satisfy 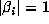 , so a bound on |a| implies
a bound on
, so a bound on |a| implies
a bound on 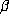 and hence on |b| and |c|. So, for fixed a, there is a finite
set of
and hence on |b| and |c|. So, for fixed a, there is a finite
set of 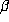 with
with 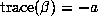 . Observe that
. Observe that

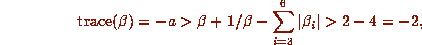 so
so 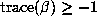 for all Salem numbers of degree 6. In fact, there are no
such numbers with trace -1, 4 with trace 0, 15 with trace 1, and 39 with
trace 2.
for all Salem numbers of degree 6. In fact, there are no
such numbers with trace -1, 4 with trace 0, 15 with trace 1, and 39 with
trace 2.
 Annotation Form Interface
Annotation Form Interface
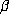 of degree 6 has a minimal polynomial of the following form:
of degree 6 has a minimal polynomial of the following form:

 where a,b and c are integers. The trace of
where a,b and c are integers. The trace of 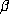 is
is
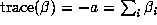 , where the sum is over the six conjugates
of
, where the sum is over the six conjugates
of 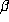 , i.e., the six roots of (2.1). Two of these conjugates are
, i.e., the six roots of (2.1). Two of these conjugates are 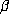 and
and
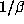 and the remaining conjugates satisfy
and the remaining conjugates satisfy 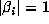 , so a bound on |a| implies
a bound on
, so a bound on |a| implies
a bound on 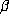 and hence on |b| and |c|. So, for fixed a, there is a finite
set of
and hence on |b| and |c|. So, for fixed a, there is a finite
set of 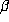 with
with 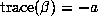 . Observe that
. Observe that

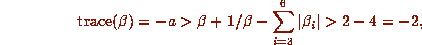 so
so 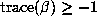 for all Salem numbers of degree 6. In fact, there are no
such numbers with trace -1, 4 with trace 0, 15 with trace 1, and 39 with
trace 2.
for all Salem numbers of degree 6. In fact, there are no
such numbers with trace -1, 4 with trace 0, 15 with trace 1, and 39 with
trace 2.