![[Shownotes]](../gif/annotate/shide-111.gif)
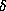 in Proposition 6.1 can plausibly be replaced by
in Proposition 6.1 can plausibly be replaced by 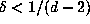 . The points
. The points 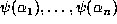 actually lie not just in a
cube
actually lie not just in a
cube 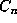 but in a slab
but in a slab 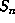 with 2 sides of bounded length, corresponding to the
conjugates
with 2 sides of bounded length, corresponding to the
conjugates 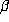 and
and 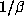 , and d-2 sides of length
, and d-2 sides of length 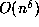 corresponding
to the conjugates
corresponding
to the conjugates 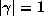 . The volume of
. The volume of 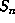 is
is 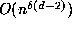 , which is
, which is
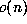 if
if 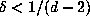 . If we assume that
. If we assume that 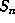 lies in ``general position'' with
respect to
lies in ``general position'' with
respect to 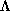 , then we would expect it to contain
, then we would expect it to contain 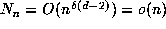 points of
points of 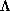 . It is possible that the slab
. It is possible that the slab 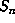 is tilted in such a way as to
contain more than its fair share of points of
is tilted in such a way as to
contain more than its fair share of points of 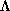 , but we regard this as unlikely.
This cannot happen with the cube
, but we regard this as unlikely.
This cannot happen with the cube 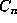 used in the proof of Proposition 6.1 and is the
reason it was used there. If the estimate
used in the proof of Proposition 6.1 and is the
reason it was used there. If the estimate 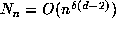 could be
established rigorously then, for d = 4, the argument here could be applied if
could be
established rigorously then, for d = 4, the argument here could be applied if 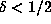 , which is almost what we get from the nonrigorous argument of .4.
, which is almost what we get from the nonrigorous argument of .4.