Assuming the orbit is randomly distributed

help

annotate

Contents Next: A random walk Up: A probabilistic model Previous: Replacing a cube

If we go beyond the box principle used in .1 and .2 and imagine that the points of the orbit

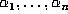are distributed ``randomly'' in the slab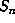

, we can allow a larger value of

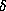. Suppose that

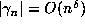with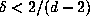

, so the volume

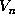of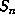

satisfies

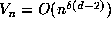and hence, as in .2,

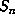contains

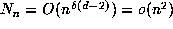points of the lattice

. Now suppose that the points

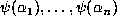are randomly chosen from these

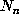points. Then, by the ``birthday paradox'' we will have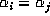

for some

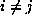with probability tending to 1 as

. That is, the probability that n randomly selected points among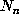

are distinct is

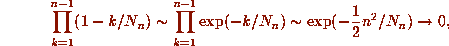as

since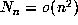

.

For d = 4, this argument requires , which is just short of what can be proved, while for d = 6, the requirement is 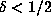, which is just short of the 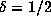we obtain in .4 by a ``random walk'' argument. For 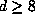, however, even the most favorable assumptions would not seem to justify the expectation that the orbit 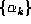should be finite.

help

annotate

Contents Next: A random walk Up: A probabilistic model Previous: Replacing a cube