![[Shownotes]](../gif/annotate/shide-141.gif)
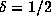 . By (6.3), we
expect that
. By (6.3), we
expect that 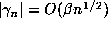 , where the O constant is uniform in
, where the O constant is uniform in
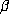 . Thus the region
. Thus the region 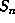 , being the product of two intervals of lengths 1 and
, being the product of two intervals of lengths 1 and
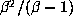 and
and 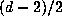 disks of radius
disks of radius 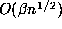 , has volume
, has volume 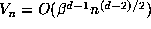 . Since the points of
. Since the points of 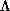 are distributed with density
are distributed with density
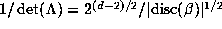 , and assuming
, and assuming 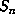 is in general
position, there are
is in general
position, there are 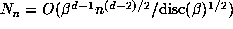 points of
points of
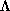 in
in 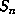 . If
. If 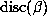 is sufficiently large, it is thus possible to
push through the argument of .2 for d = 4 and the birthday paradox argument of
.3 for d = 6 to conclude that the orbit of
is sufficiently large, it is thus possible to
push through the argument of .2 for d = 4 and the birthday paradox argument of
.3 for d = 6 to conclude that the orbit of 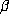 should be finite.
should be finite.

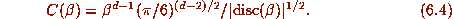 If
If 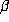 is large, then the largest terms in
is large, then the largest terms in 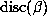 are the d-1 terms
involving the conjugate
are the d-1 terms
involving the conjugate 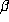 ; their product is about
; their product is about 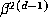 . If the
conjugates on the unit circle are nicely distributed, then we would expect the product of
terms involving them not to be too small and so ``typically''
. If the
conjugates on the unit circle are nicely distributed, then we would expect the product of
terms involving them not to be too small and so ``typically'' 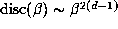 and
and 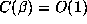 from (6.4). Values of
from (6.4). Values of 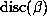 which
are untypically small will lead to large values of
which
are untypically small will lead to large values of 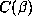 .
.