![[Shownotes]](../gif/annotate/sshow-31.gif)
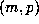 for these numbers
is quite remarkable. For the most part there is a great deal of regularity, and the
values of m and p are quite small: for all but 199 of the numbers surveyed, both
m < 1000 and p < 1000. For 9609 of the numbers (81% of the total) we
have m = 1, but, in contrast to the degree-4 situation, larger values of m do
occur with a certain regularity. However, among the remaining 199 cases, there are
at least 79 for which
for these numbers
is quite remarkable. For the most part there is a great deal of regularity, and the
values of m and p are quite small: for all but 199 of the numbers surveyed, both
m < 1000 and p < 1000. For 9609 of the numbers (81% of the total) we
have m = 1, but, in contrast to the degree-4 situation, larger values of m do
occur with a certain regularity. However, among the remaining 199 cases, there are
at least 79 for which 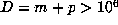 and at least two for which
and at least two for which 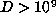 .
.
The two known examples with 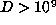 are
are 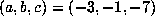 and
and
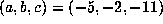 . This might suggest that these
. This might suggest that these 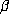 are not beta numbers. However,
there are some very large values of m and p among the cases where
are not beta numbers. However,
there are some very large values of m and p among the cases where 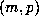 has been
determined. The (current) record is attained for
has been
determined. The (current) record is attained for 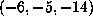 , which has
, which has
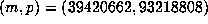 . Other notable values are
. Other notable values are 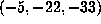 with
with
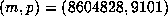 , and
, and 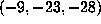 with
with 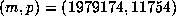 .
.
A sample of these numerical results is presented in two tables organized as follows. In
Table 1 of the Supplement all quintuples 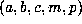 with
with 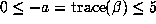 are listed, provided both m < 10000 and p < 10000. The complete table for
are listed, provided both m < 10000 and p < 10000. The complete table for 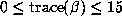 is over 20 times longer than that presented here and has much
the same general appearance. Table 2 of the Supplement gives the 36 values
is over 20 times longer than that presented here and has much
the same general appearance. Table 2 of the Supplement gives the 36 values 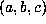 with
with 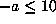 for which
for which 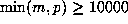 . This includes 18 cases where only a
lower bound for D = m+p is known.
. This includes 18 cases where only a
lower bound for D = m+p is known.
Although there must be other factors involved, the argument of
§ 6 suggests that the
size of 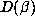 is directly related to the size of
is directly related to the size of
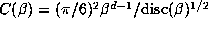 . In particular, numbers
with smaller discriminants should have larger orbits. The prediction of § 6.6 is that
the orbit will be finite provided
. In particular, numbers
with smaller discriminants should have larger orbits. The prediction of § 6.6 is that
the orbit will be finite provided 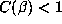 . We illustrate this in Table 3, where
we list the values of
. We illustrate this in Table 3, where
we list the values of 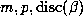 and
and 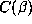 for the 11 Salem numbers
with a = -3, b=-1, so
for the 11 Salem numbers
with a = -3, b=-1, so 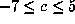 . The omitted values of c correspond to
reducible polynomials.
. The omitted values of c correspond to
reducible polynomials.
One might expect that the size of the period of 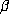 might depend on arithmetic
properties of
might depend on arithmetic
properties of 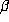 or perhaps on the existence of approximate multiplicative
relationships between the conjugates
or perhaps on the existence of approximate multiplicative
relationships between the conjugates 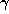 of
of 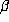 with
with 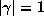 . If this
were true, then one would expect powers of
. If this
were true, then one would expect powers of 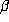 to behave in a manner similar to
to behave in a manner similar to
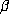 . A counterexample to this expectation is the
. A counterexample to this expectation is the 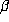 with
with 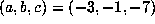 , where
, where 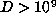 . Here,
. Here, 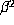 has
has 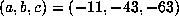 with
with 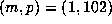 .
.
Exploring this theme further, we consider the powers of the smallest Salem number of
degree 6, 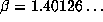 , which has
, which has 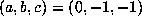 . For
. For 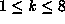 ,
Table 4 gives
,
Table 4 gives 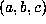 for the minimal polynomial of
for the minimal polynomial of 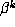 , the values of m and
p,
, the values of m and
p, 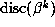 and
and 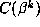 . The factored form of
. The factored form of 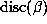 is given
for the sake of interest, although the arithmetic properties of
is given
for the sake of interest, although the arithmetic properties of 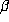 appear to play
no role here.
Table 4 (powers of
appear to play
no role here.
Table 4 (powers of 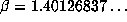 )
)