![[Shownotes]](../gif/annotate/shide-61.gif)
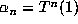 for
for 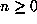 , and
, and 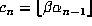 for
for 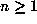 . Consider first how one would compute
these quantities using an approximation to the real number
. Consider first how one would compute
these quantities using an approximation to the real number 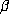 . If an approximation
. If an approximation
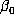 to
to 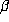 is used which has
is used which has 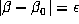 , then the error in
the corresponding approximation to
, then the error in
the corresponding approximation to 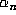 is about
is about 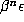 . Thus, for
large n it will be impossible to compute
. Thus, for
large n it will be impossible to compute 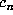 correctly. In addition, even for small
n, it would be impossible to decide whether or not
correctly. In addition, even for small
n, it would be impossible to decide whether or not 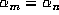 for some
for some 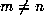 .
.
On the other hand, if 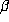 is an algebraic integer, then all
is an algebraic integer, then all 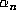 lie in
lie in
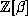 . Specifically, if
. Specifically, if 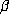 has degree d and minimal polynomial P,
and if
has degree d and minimal polynomial P,
and if 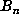 is the polynomial of degree d-1 definied by
is the polynomial of degree d-1 definied by 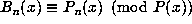 , where
, where 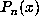 is as in § 1, then
is as in § 1, then 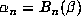 . The
. The 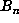 thus
provide an exact representation of
thus
provide an exact representation of 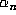 , so the question
, so the question 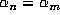 can
be effectively answered. Since the
can
be effectively answered. Since the 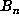 satisfy the recurrence
satisfy the recurrence

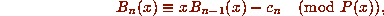 the computation simply involves a shift
of the coefficients of
the computation simply involves a shift
of the coefficients of 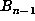 followed by the replacement of
followed by the replacement of 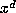 by
by 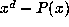 .
.
The only difficulty is the determination of 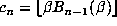 . This can be computed using an approximation
. This can be computed using an approximation 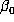 to
to 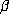 of modest
accuracy unless
of modest
accuracy unless 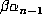 is unusually close to an integer c. If
is unusually close to an integer c. If 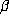 is a Salem number, standard arguments from transcendence theory show that
is a Salem number, standard arguments from transcendence theory show that

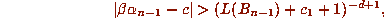 where
where 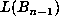 denotes
the sum of the absolute values of the coefficients of
denotes
the sum of the absolute values of the coefficients of 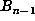 . One simply observes
that there is an obvious bound on the conjugates of
. One simply observes
that there is an obvious bound on the conjugates of 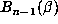 owing to the fact
that the other conjugates of
owing to the fact
that the other conjugates of 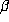 all have absolute value
all have absolute value 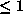 , and that the
product of all the conjugates is a nonzero integer.
, and that the
product of all the conjugates is a nonzero integer.
In practice, we can simply choose an approximation 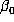 to
to 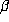 of fixed
accuracy
of fixed
accuracy  . (We usually chose
. (We usually chose  to be
to be 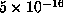 or
or 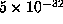 .) The number
.) The number 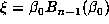 is an approximation to
is an approximation to
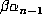 whose accuracy is easily estimated. If
whose accuracy is easily estimated. If 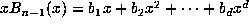 , and if
, and if 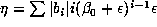 , then
, then
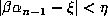 . Thus, if the distance from
. Thus, if the distance from 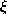 to the nearest
integer is at least
to the nearest
integer is at least 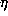 , then
, then 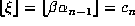 .
.
Our algorithm begins with 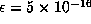 (double precision). If at
some point in the computation, the criterion of the previous paragraph fails, the
computation of
(double precision). If at
some point in the computation, the criterion of the previous paragraph fails, the
computation of 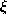 is repeated with a
is repeated with a 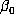 having accuracy
having accuracy 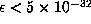 (quadruple precision). If the criterion fails at this level of accuracy, then
the computation is terminated. This occurred for only five values of
(quadruple precision). If the criterion fails at this level of accuracy, then
the computation is terminated. This occurred for only five values of 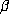 in our
entire project, one of which can be recognized in Table 2:
in our
entire project, one of which can be recognized in Table 2: 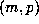 is not given, but the
corresponding lower bound on D is
is not given, but the
corresponding lower bound on D is 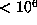 .
For each
.
For each 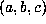 , the values of n for which a change from double precision to
quadruple precision was necessary were recorded in a file during the computation. We
indicate below how these values were used in some cases to determine some of the larger
values of
, the values of n for which a change from double precision to
quadruple precision was necessary were recorded in a file during the computation. We
indicate below how these values were used in some cases to determine some of the larger
values of 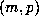 .
.
As a sample of the accuracy needed, suppose we were to take 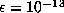 for
the
for
the 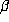 with
with 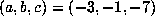 . Then for n = 167305 one computes
. Then for n = 167305 one computes 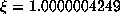 , suggesting that
, suggesting that 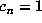 , while in fact
, while in fact 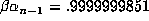 , so
, so 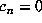 . On the other hand, for most values of n, a far less
accurate value of
. On the other hand, for most values of n, a far less
accurate value of 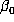 would suffice. The two-tier arrangement described in the
previous paragraph allows one to make use of the fast double-precision multiplication on
the machine used (an Amdahl 5860) while retaining the benefits of a higher-precision
calculation when required. One could easily envision a multiple-tier approach.
The sequence
would suffice. The two-tier arrangement described in the
previous paragraph allows one to make use of the fast double-precision multiplication on
the machine used (an Amdahl 5860) while retaining the benefits of a higher-precision
calculation when required. One could easily envision a multiple-tier approach.
The sequence 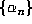 is periodic if and only if
is periodic if and only if 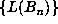 is bounded. Thus,
if
is bounded. Thus,
if 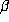 is a beta number, its expansion can be computed using an approximation
is a beta number, its expansion can be computed using an approximation
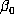 of some fixed accuracy (which depends on
of some fixed accuracy (which depends on 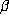 , of course).
, of course).