Robert M. Corless
Dept. Applied Math
University of Western Ontario
London, Ontario
Canada
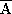 ryabhata, and possibly as far back as
c. 300 B.C. to Euclid. The theory of chaotic dynamical systems is
relatively recent, going back only to the work of
Poincaré [20] and
Birkhoff [2]. The foundations of the theory of continued fractions,
as we know it now, are well established due to the work of Euler, Lagrange,
Gauss, and others, while the foundations of chaotic dynamical systems are
still evolving. This paper will use the well-established theory of simple
continued fractions to explore some current results of the theory of chaotic
dynamical systems.
ryabhata, and possibly as far back as
c. 300 B.C. to Euclid. The theory of chaotic dynamical systems is
relatively recent, going back only to the work of
Poincaré [20] and
Birkhoff [2]. The foundations of the theory of continued fractions,
as we know it now, are well established due to the work of Euler, Lagrange,
Gauss, and others, while the foundations of chaotic dynamical systems are
still evolving. This paper will use the well-established theory of simple
continued fractions to explore some current results of the theory of chaotic
dynamical systems.
The paper was written because of efforts on my part to learn about
chaos.
In taking Paddy Nerenberg's course on chaos, I was reminded of efforts
to compute the continued fraction for  in George Maxwell's number
theory class when I was an undergraduate: the behaviour of the algorithm
for computing the continued fraction led to just the same sorts of
divergences
that I was seeing in computing the chaotic maps in the course.
The paper was a fairly natural outgrowth of that observation, and
I gave my first talk at the Ontario Mathematics Meeting in 1988 on
this topic (it was a miserable talk---among other things, I committed
the cardinal sin of going over time).
in George Maxwell's number
theory class when I was an undergraduate: the behaviour of the algorithm
for computing the continued fraction led to just the same sorts of
divergences
that I was seeing in computing the chaotic maps in the course.
The paper was a fairly natural outgrowth of that observation, and
I gave my first talk at the Ontario Mathematics Meeting in 1988 on
this topic (it was a miserable talk---among other things, I committed
the cardinal sin of going over time).
There are plenty of places where stylistic improvements to the paper can be made, and I have taken this opportunity to make some of them. In particular, Nick Higham used one pair of sentences from this paper as a `bad example', in his book `Handbook of Mathematical Writing'. Oops, heh-heh, pardon me while I fix that...
In addition, the paper has been thoroughly read by Dhavide Aruliah, Heinz Bauschke, Greg Fee, and Jennifer Overington, who have all made stylistic comments. Dhavide and Jennifer have taken material I had written for talks and workshops, subsequent to the writing of CFC, and used them in part to create tutorials on continued fractions and on chaos (in particular on Lyapunov exponents). It is my hope that these tutorials will be hooked up in a useful way to this paper. Greg Fee dug out and implemented Floyd's algorithm from Knuth, vol II, for identifying the start of a cycle in a map, and this enables us to investigate the floating-point Gauss map even more thoroughly. All of this has helped to make this electronic version not just an updated and corrected version, but one with more content, as well.
As far as the content goes, I found in re-reading it, and adapting it to this electronic medium, that my ideas and knowledge about chaos have grown and changed considerably. In particular, I know a lot more now about shadowing and its importance for computation.
Nevertheless the ideas expressed in this paper remain, at least in embryo, central to my view of reliable and faithful simulation of chaotic dynamical systems. I have followed this paper with several related ones, but the main candidate to be called a proper sequel to this paper is `What Good are Numerical Simulations of Chaotic Dynamical Systems', which appeared this year (1995) in Computers and Mathematics with Applications.
In `What Good' I am concerned chiefly with the fidelity of numerical methods for solving nonlinear ordinary differential equations, and the ideas brought forth in CFC really help to explain the problem that I'm looking at, and also the remaining unresolved problems. You see, if we had a good general understanding of the methods for solving such problems, then we ought to understand the numerical simulation of the Gauss map; but we don't really understand why it works. In CFC I was groping towards understanding what we don't understand: I say in CFC that `On closer examination, however, we see that if the period of an orbit is long, then the orbit behaves for a long time as if it were aperiodic, reflecting the effect of ``nearby'' initial points that are aperiodic.'
I believe this statement to be true, and there is a theorem
of Gora and Boyarsky which helps me with that belief. But the
point is still not established rigorously, and it seems to me that
this is still the central issue with the fidelity of numerical methods.
Floating-point arithmetic is finite, and this has serious consequences
for modelling the infinite (or at least it ought to, and sometimes it
does). We really need a good theory to explain why these mathematical
experiments really work (the computation of 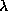 in this paper).
The trick will be in showing that the statistics (distributions) of the
orbits will be mostly right if the local accuracy of the computation
of the map is high; note that this is a discrete `local to global'
problem, and the results of Gora and Boyarsky are the best in this
context to date (they still don't explain the Gauss map results,
though). This question must be answered before we can place any
faith in the computation of Lyapunov exponents for nonlinear problems,
for example. Shadowing helps, but is not enough.
in this paper).
The trick will be in showing that the statistics (distributions) of the
orbits will be mostly right if the local accuracy of the computation
of the map is high; note that this is a discrete `local to global'
problem, and the results of Gora and Boyarsky are the best in this
context to date (they still don't explain the Gauss map results,
though). This question must be answered before we can place any
faith in the computation of Lyapunov exponents for nonlinear problems,
for example. Shadowing helps, but is not enough.
So the connection of this paper to Experimental Mathematics is, in some sense, a question of the validation of the tools that we are using with Experimental Mathematics (at least for the simulation of chaotic maps or odes).
Aside from that, computation with the Gauss map leads directly to almost all of the main ideas in chaotic dynamical systems: ergodicity, Markov partitions, shadowing, Lyapunov exponents, reliability of simulation. So in some sense it provides a `Royal Road' to chaos.
Some other questions that asked themselves of me while I re-read this paper are
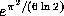 the P-th root of
a quadratic irrational? It's not known if it's
algebraic, but perhaps this weaker result is known?
This is a question that can be `experimentally' answered, at least
for polynomial coefficients up to a certain size. Then I could
remove the footnote that a last-minute editor or referee put in to
my paper about this, and fix a typo which caused the referee to put
the footnote there...
the P-th root of
a quadratic irrational? It's not known if it's
algebraic, but perhaps this weaker result is known?
This is a question that can be `experimentally' answered, at least
for polynomial coefficients up to a certain size. Then I could
remove the footnote that a last-minute editor or referee put in to
my paper about this, and fix a typo which caused the referee to put
the footnote there...
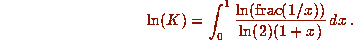
We can now compute  quickly, using a rather fast series. Can
this integral be computed quickly any other way? There are an infinite
number of ever-weakening jump discontinuities near the origin.
quickly, using a rather fast series. Can
this integral be computed quickly any other way? There are an infinite
number of ever-weakening jump discontinuities near the origin.
And by the way, what is the official spelling of Khinchin? I don't use the t, because it didn't appear on his book. But it is spelled differently in many places in the literature, in English. Now that TeX is available, perhaps we can spell it correctly in the Cyrillic alphabet?
All in all, I am very grateful for the chance to revisit this paper, particularly in such company. The prizes won by the other authors in this volume for expository writing include the Chauvenet Prize (Borwein, Borwein, and Bailey, 1992), the Lester R. Ford Award (Jeffrey Lagarias, 1985; Stan Wagon, 1988; Ronald L. Graham, 1991), and the Carl Allendoerfer Award (Ronald L. Graham, 1990). Doubtless by the time you read this other authors in the volume will have won more---it really is an all-star lineup.