All of the results of the previous sections are valid for the
familiar domain of the real numbers. However, when we work in
any fixed-precision
system, we have two difficulties:
- Not all numbers are even representable in the system, and
- Arithmetic doesn't have the properties we are used to.
For example, defining u as the smallest machine representable
number which when added to 1 gives a number different from 1
when stored, we see that 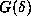 is computed as 0, whenever
is computed as 0, whenever
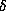 is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.
is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.
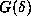 is computed as 0, whenever
is computed as 0, whenever
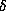 is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.
is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.