The following theorem justifies the remarks of the previous section.
The basic idea of its proof is that given some initial point 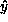 the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to
the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to 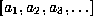 , where the
, where the 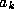 are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the
are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the 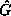 -orbit
of
-orbit
of 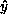 . The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
. The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
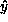 the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to
the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to 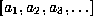 , where the
, where the 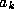 are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the
are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the 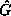 -orbit
of
-orbit
of 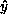 . The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
. The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).