We begin with the classical method for finding the continued fraction
representation of a number 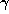 . We put
. We put 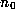 equal to the integer
part of
equal to the integer
part of 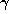 , by which we mean the greatest integer less than or
equal to
, by which we mean the greatest integer less than or
equal to 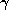 . If the fractional part of
. If the fractional part of 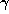 is not zero, we
put
is not zero, we
put 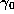 equal to the fractional part of
equal to the fractional part of 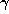 . We then
invert
. We then
invert 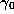 , and put
, and put 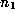 equal to the integer part of
equal to the integer part of 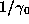 .
Similarly we put
.
Similarly we put 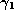 equal to the fractional part, and repeat.
Note that
equal to the fractional part, and repeat.
Note that 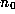 may be positive, negative, or zero, but that all the
subsequent
may be positive, negative, or zero, but that all the
subsequent 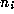 will be positive, and that each
will be positive, and that each 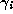 is in the
interval
is in the
interval 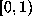 .
This process gives us a unique continued fraction for each starting point
.
This process gives us a unique continued fraction for each starting point
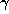 , and the process terminates if and only if
, and the process terminates if and only if 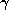 is rational.
(For any rational
is rational.
(For any rational 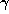 there is one other simple continued fraction, e.g.
there is one other simple continued fraction, e.g. 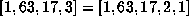 ,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of
,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of 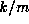 , then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in
, then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in 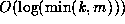 operations.
operations.
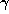 . We put
. We put 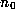 equal to the integer
part of
equal to the integer
part of 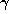 , by which we mean the greatest integer less than or
equal to
, by which we mean the greatest integer less than or
equal to 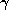 . If the fractional part of
. If the fractional part of 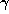 is not zero, we
put
is not zero, we
put 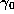 equal to the fractional part of
equal to the fractional part of 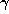 . We then
invert
. We then
invert 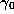 , and put
, and put 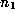 equal to the integer part of
equal to the integer part of 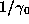 .
Similarly we put
.
Similarly we put 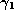 equal to the fractional part, and repeat.
Note that
equal to the fractional part, and repeat.
Note that 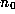 may be positive, negative, or zero, but that all the
subsequent
may be positive, negative, or zero, but that all the
subsequent 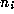 will be positive, and that each
will be positive, and that each 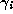 is in the
interval
is in the
interval 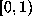 .
This process gives us a unique continued fraction for each starting point
.
This process gives us a unique continued fraction for each starting point
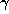 , and the process terminates if and only if
, and the process terminates if and only if 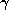 is rational.
(For any rational
is rational.
(For any rational 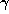 there is one other simple continued fraction, e.g.
there is one other simple continued fraction, e.g. 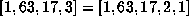 ,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of
,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of 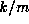 , then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in
, then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in 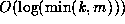 operations.
operations.