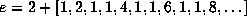 .
The elements of the orbit of this initial point are always of the form
.
The elements of the orbit of this initial point are always of the form
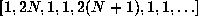 ,
, 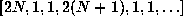 ,
or
,
or 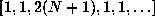 ,
which tend to 1, 0, and
,
which tend to 1, 0, and 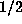 , respectively. Thus the
, respectively. Thus the
 -limit set
of this orbit is the set
-limit set
of this orbit is the set 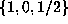 , which, unlike the
, which, unlike the  -
limit sets of continuous maps, is not invariant
under the Gauss
map since
-
limit sets of continuous maps, is not invariant
under the Gauss
map since 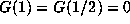 so G applied to this set simply gives
0. In other words, we have an
asymptotically periodic orbit which is
not asymptotic to a real orbit of the map. This cannot happen for a
discrete dynamical system with a continuous map.
so G applied to this set simply gives
0. In other words, we have an
asymptotically periodic orbit which is
not asymptotic to a real orbit of the map. This cannot happen for a
discrete dynamical system with a continuous map.
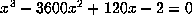 , then
, then

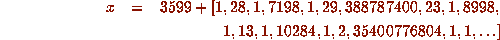 which has very large entries placed irregularly throughout. This
intermittency is a typical feature of a chaotic system [10].
which has very large entries placed irregularly throughout. This
intermittency is a typical feature of a chaotic system [10].
 are thus aperiodic. We
examine some beautiful examples, beginning with one due to Euler:
are thus aperiodic. We
examine some beautiful examples, beginning with one due to Euler: