One might ask if there are non-noble numbers with this
Lyapunov exponent, and indeed I think the answer is yes. The trick to
this is constructing numbers with lots of 1's in the continued
fraction. For example, 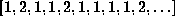 ,
where there are
,
where there are 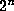 1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.
1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.
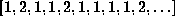 ,
where there are
,
where there are 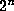 1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.
1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.