

Contents
Next: Example
Up: Orbits under are
Previous: Orbits under are
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-131.gif)
This shadowing result is very strong, because it is special to the
Gauss map. We have shown that every computed orbit is
uniformly shadowed by a true orbit for all iterations,
and that the distance to the true orbit is uniformly bounded by a small
multiple of the machine epsilon u. (Incidentally, I now believe
(1995) that we can replace the 4 in the above with 2, but it's not worth
writing the changes down, really). Most general shadowing results seem to hold only for
finite times, and have bounds more like 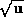 . Most computational
procedures for a posteriori verification of shadowing also fit this
model.
. Most computational
procedures for a posteriori verification of shadowing also fit this
model.


Contents
Next: Example
Up: Orbits under are
Previous: Orbits under are
![[Shownotes]](../gif/annotate/sshow-131.gif)
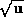 . Most computational
procedures for a posteriori verification of shadowing also fit this
model.
. Most computational
procedures for a posteriori verification of shadowing also fit this
model.