![[Shownotes]](../gif/annotate/shide-91.gif)
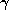 in
in 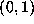 with this Lyapunov exponent. For example, all the numbers
with this Lyapunov exponent. For example, all the numbers
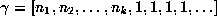 , that is, all the
numbers whose continued fractions ultimately end in 1's, have Lyapunov
exponent
, that is, all the
numbers whose continued fractions ultimately end in 1's, have Lyapunov
exponent  . These are the so-called noble
numbers [25], noticed for their resistance to chaos,
and we see here that they all
share the (still positive) minimum possible Lyapunov exponent
under the Gauss map.
. These are the so-called noble
numbers [25], noticed for their resistance to chaos,
and we see here that they all
share the (still positive) minimum possible Lyapunov exponent
under the Gauss map.
One might ask if there are non-noble numbers with this
Lyapunov exponent, and indeed I think the answer is yes. The trick to
this is constructing numbers with lots of 1's in the continued
fraction. For example, 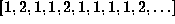 ,
where there are
,
where there are 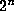 1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.
1's in between the 2's, might work.
I do not know of
a good characterization of the set of all such noble-equivalent or
`nearly noble'
numbers.