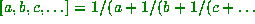 .
.
Robert M. Corless
today
When I first wrote ``Chaos and Continued Fractions'', I thought that nobody would be interested in the details of the induction used to prove the connection between G and the shift map. Indeed, I didn't write out the induction formally myself, just doing it `in my head'.
But Julian Palmore was disappointed in me for not giving the details, and likewise Heinz Bauschke. Neither of these people has the slightest need for the details, being well able to fill them in, but it's clear that they wanted to see them.
In retrospect, I agree: inductive proofs are among the prettiest there are, and a short induction proving something interesting, or a delicate induction showing something difficult, are both welcome items in a mathematical paper. This is a lesson in expository writing of mathematics, which I have now taken to heart.
For this particular example, I don't think induction is really necessary---at least, the induction part is trivial, so I really shouldn't have used the word (and got my readers' hopes up). But here we use induction to establish something, anyway.
Remember that in our notation, 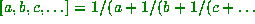 .
.
Theorem: If 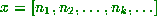 , then
, then
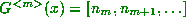 for every possible integer
for every possible integer 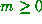 (i.e. if x is rational, then
(i.e. if x is rational, then  where N is the order of the continued fraction, but if x is irrational, then m is not bounded).
where N is the order of the continued fraction, but if x is irrational, then m is not bounded).
Proof: The statement is true for m = 0. Assume that it is true
for m = k and consider 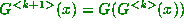 . By
the inductive hypothesis,
. By
the inductive hypothesis,
 or, in fractional notation,
or, in fractional notation,
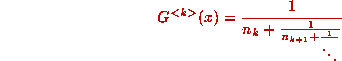 Taking reciprocals, we have
Taking reciprocals, we have
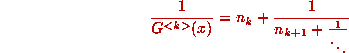 and taking the fractional part (remember
and taking the fractional part (remember 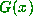 is the
fractional part of
is the
fractional part of 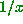 , so we have just computed
, so we have just computed  ) gives us
) gives us 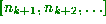 . Thus
. Thus 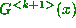 has the correct form, and this completes the proof.
has the correct form, and this completes the proof.
Remark. The proof relies on the fact that the objects being
manipulated are well-defined. That this is so follows from the
convergence of infinite continued fractions, and is trivial in the
case of finite continued fractions.