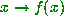 here, with orbit
here, with orbit 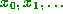 where
where 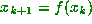 as usual.
as usual.
Robert M. Corless
Tue Nov 28 18:16:03 PST 1995
In ``Continued Fractions and Chaos'' I used, without explanation, the following definition of S.I.C. or Sensitive to Initial Conditions. It seemed to me to be obviously equivalent. On thinking about it a bit more, it's not so obvious, but it is indeed a useful way of looking at it. For example, unlike the Lyapunov exponent definition, it does not require any smoothness of f at all. Besides, I have not seen this definition elsewhere in the literature and so it might be as well to write it down explicitly.
We suppose that we are iterating a map 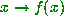 here, with orbit
here, with orbit 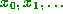 where
where 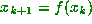 as usual.
as usual.
Definition. A map f is S.I.C. if for almost all 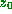 in the domain of f
there exist constants
in the domain of f
there exist constants 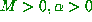 , and
, and
 such that for all
such that for all 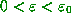 there exist
there exist 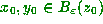 (the ball of radius
(the ball of radius  around
around 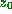 ) such that for some
) such that for some 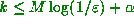 we have
we have 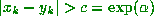 .
.
Roughly speaking, 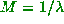 , where
, where  is the Lyapunov exponent, and
if we have exponential separation of orbits, then
is the Lyapunov exponent, and
if we have exponential separation of orbits, then 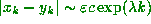 ,
(at least until the nonlinearities and boundedness takes over---a better formulation
of Lyapunov exponent looks directly at the tangent space, whereas we are looking here at
the actual orbits) which is the usual definition of S.I.C. if
,
(at least until the nonlinearities and boundedness takes over---a better formulation
of Lyapunov exponent looks directly at the tangent space, whereas we are looking here at
the actual orbits) which is the usual definition of S.I.C. if  . If we plug in
the k from the above definition we get
. If we plug in
the k from the above definition we get 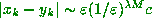 which, if we take
which, if we take  , gives us the required behaviour.
, gives us the required behaviour.
In shorthand notation we say that points initially 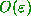 apart become
apart become 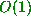 apart
after
apart
after 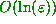 iterations of the map. In some ways this is an easier definition
to work with than the usual one, which requires investigations of limits in tangent
space (i.e. calculation of the Lyapunov exponent), which may or may not even
exist for a large number of orbits. In my view it is superior to some other
definitions of S.I.C. (such as Wiggins' definition) which do not require separation
at an exponential rate. To me, as it was to Paddy Nerenberg, it is the exponential
rate that makes a map `sensitive', because algebraic separation is usually by far
the less spectacular. However, I acknowledge that so long as we are clear about
which definition is being used, different definitions can be used in different contexts,
as appropriate.
iterations of the map. In some ways this is an easier definition
to work with than the usual one, which requires investigations of limits in tangent
space (i.e. calculation of the Lyapunov exponent), which may or may not even
exist for a large number of orbits. In my view it is superior to some other
definitions of S.I.C. (such as Wiggins' definition) which do not require separation
at an exponential rate. To me, as it was to Paddy Nerenberg, it is the exponential
rate that makes a map `sensitive', because algebraic separation is usually by far
the less spectacular. However, I acknowledge that so long as we are clear about
which definition is being used, different definitions can be used in different contexts,
as appropriate.
What we proved in the paper was that we could take M from the known speed of
the Euclidean algorithm, and choose 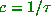 . In fact,
. In fact, 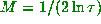 can
be explicitly inferred from the minimal Lyapunov exponent theorem of the paper.
So for the Gauss map, the results are uniform, in some sense. Indeed, we can also
take
can
be explicitly inferred from the minimal Lyapunov exponent theorem of the paper.
So for the Gauss map, the results are uniform, in some sense. Indeed, we can also
take  , the width of the entire interval.
, the width of the entire interval.
For the shift map 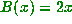 mod 1, this definition is also easy to use, and
I recommend the reader show that this map is S.I.C. as an exercise.
mod 1, this definition is also easy to use, and
I recommend the reader show that this map is S.I.C. as an exercise.