




Next: About this document
The Machine Epsilon
Robert M. Corless
Tue Nov 28 18:19:22 PST 1995
The definition of the `machine epsilon' u given in the paper `Chaos and Continued
Fractions' is the standard one used in numerical analysis. However, it is a bit tricky
to understand for people not used to floating-point arithmetic, and is especially tricky
in Maple because the value of u depends on the setting of Digits and also on whether
or not hardware floating point (evalhf) is being used.
The definition is `the smallest number u which when added to 1 gives
something different than 1'. Of course, in the real number system, this could
only be u = 0, and indeed the machine epsilon acts something like zero in some
cases in floating point systems. But in floating point, u is not zero, because
of rounding. Moreover, u is not the smallest floating point number we
can represent, as we will see.
Let us suppose we are working in Maple to 6 Digits. Then if we add 5.0*10^(-Digits)
to 1, we get  as our result. Maple internally computed
as our result. Maple internally computed  and
then rounded to 6 Digits, to get that answer. If now we add
and
then rounded to 6 Digits, to get that answer. If now we add 4.99999*10^(-Digits)
to 1, we get  , which really is 1. Maple internally computed the result
to a higher precision, and then (correctly) rounded the result. So here, u is
, which really is 1. Maple internally computed the result
to a higher precision, and then (correctly) rounded the result. So here, u is
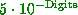 . Things get more complicated when
. Things get more complicated when evalhf
is involved.
But of course we can represent smaller numbers:  , for
example, is a perfectly representable number in Maple to 6 Digits. The difference is
that the exponent (here 200) is independent of the number of digits in the `significand'
, for
example, is a perfectly representable number in Maple to 6 Digits. The difference is
that the exponent (here 200) is independent of the number of digits in the `significand'
 (older works called this the `mantissa' but the current, more rational,
practice is to use the word `significand').
(older works called this the `mantissa' but the current, more rational,
practice is to use the word `significand').
The importance of the machine epsilon is that it measures the effects of rounding
errors made when adding, subtracting, multiplying, or dividing two numbers. No
matter how carefully you do any of these operations, you must make an error at
least this big (in a relative sense) when you round your answer to the number of
Digits you are using.





Next: About this document
 as our result. Maple internally computed
as our result. Maple internally computed  and
then rounded to 6 Digits, to get that answer. If now we add
and
then rounded to 6 Digits, to get that answer. If now we add  , which really is 1. Maple internally computed the result
to a higher precision, and then (correctly) rounded the result. So here, u is
, which really is 1. Maple internally computed the result
to a higher precision, and then (correctly) rounded the result. So here, u is
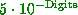 . Things get more complicated when
. Things get more complicated when 
