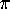 . Although Ramanujan
did not know these algorithms many of the key ingredients
are in his notebooks [13]. The algorithms depend crucially
on the solvable forms of certain modular equations for the theta-functions
due to Ramanujan. In [8] two algorithms are given --
one quartic and one quintic algorithm. In a related paper [5]
a septic algorithm is sketched. In [4] a general method is
given for constructing p-th order algorithms. These algorithms involve defining
a sequence
. Although Ramanujan
did not know these algorithms many of the key ingredients
are in his notebooks [13]. The algorithms depend crucially
on the solvable forms of certain modular equations for the theta-functions
due to Ramanujan. In [8] two algorithms are given --
one quartic and one quintic algorithm. In a related paper [5]
a septic algorithm is sketched. In [4] a general method is
given for constructing p-th order algorithms. These algorithms involve defining
a sequence 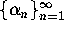 recursively and for which
recursively and for which
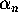 converges to
converges to 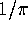 to high order.
In
general, for us, p-th order convergence of a sequence
to high order.
In
general, for us, p-th order convergence of a sequence 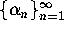 to
to  means that
means that 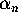 tends to
tends to 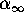 and that
and that

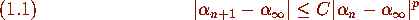 for some constant C>0. The proof of p-th order convergence
depends crucially on identifying
for some constant C>0. The proof of p-th order convergence
depends crucially on identifying 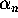 as the value of a certain
function
as the value of a certain
function 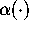 , which can be defined in terms of elliptic
integrals or equivalently in terms of theta-functions.
, which can be defined in terms of elliptic
integrals or equivalently in terms of theta-functions.