
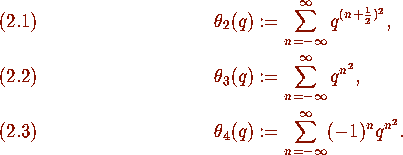 The alpha-function can be defined as
The alpha-function can be defined as

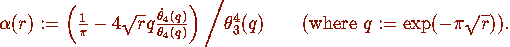 As r tends to infinity we see that q tends to zero so that
we have
As r tends to infinity we see that q tends to zero so that
we have

 In [8, Theorem 3, p. 215,] Borwein, Borwein and Bailey are able
to express
In [8, Theorem 3, p. 215,] Borwein, Borwein and Bailey are able
to express 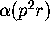 in terms of
in terms of 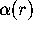 and various theta
functions. Utilizing p-th order modular equations for the theta
functions, they then are able to construct p-th order iterations
that converge to
and various theta
functions. Utilizing p-th order modular equations for the theta
functions, they then are able to construct p-th order iterations
that converge to 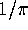 . In the next section we show how
to construct p-th order iterations in a different way. Instead
of a single alpha-function we construct an infinite family
of functions
. In the next section we show how
to construct p-th order iterations in a different way. Instead
of a single alpha-function we construct an infinite family
of functions 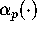 .
.