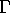 denote the classical modular group, ie. the
group of
denote the classical modular group, ie. the
group of 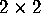 matrices with integer coefficients with
determinant +1. The elements of
matrices with integer coefficients with
determinant +1. The elements of 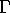 act on a given
binary quadratic form in a natural way. Consider the form
act on a given
binary quadratic form in a natural way. Consider the form
We let 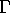 denote the classical modular group, ie. the
group of
denote the classical modular group, ie. the
group of 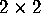 matrices with integer coefficients with
determinant +1. The elements of
matrices with integer coefficients with
determinant +1. The elements of 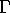 act on a given
binary quadratic form in a natural way. Consider the form
act on a given
binary quadratic form in a natural way. Consider the form

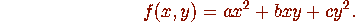 The matrix
The matrix

 acts on f as follows. Under the transformation
acts on f as follows. Under the transformation

 the form f is transformed into the form
the form f is transformed into the form

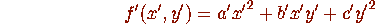 where
where

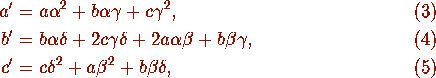 and
and 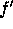 has discriminant
has discriminant

 This defines an equivalence relation
This defines an equivalence relation 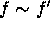 . Also note that the discriminant
is invariant. The number of equivalence classes of forms of a given
discriminant
. Also note that the discriminant
is invariant. The number of equivalence classes of forms of a given
discriminant 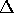 , is called the class number
, is called the class number
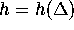 . Below is table of class numbers for forms with negative
discriminant.
. Below is table of class numbers for forms with negative
discriminant.