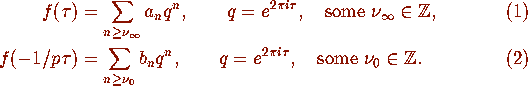is
said to be a modular function on the congruence subgroup
is
said to be a modular function on the congruence subgroup  if it
satisfies the following conditions:
if it
satisfies the following conditions:
Let p be prime. A function  is
said to be a modular function on the congruence subgroup
is
said to be a modular function on the congruence subgroup  if it
satisfies the following conditions:
if it
satisfies the following conditions:
 ,
,
 for all
for all  ,
,
 for
for  ; i.e.
; i.e.  has the form
has the form  for some
for some
 where
where  .
.