



Contents
Next: About this document
Up: Arithmetic Properties of Binomial
Previous: Bibliographic material
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-151.gif)
References
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-152.gif)
- 1
- G. Almkvist and A. Meurman,
Values of Bernoulli polynomials and Hurwitz's zeta function at rational points, C.R. Math. Acad. Sci. Canada, 13 (1991), 104--108.
[1]
- 2
- D.W. Boyd, J. Cook and P. Morton,
On sequences of
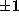 's defined by binary patterns,
Diss. Math., 283, 60pp.
's defined by binary patterns,
Diss. Math., 283, 60pp.
[1] [2]
- 3
- S. Chowla, B. Dwork and R. Evans,
On mod
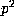 determination of
determination of 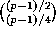 ,
J. of Number Theory, 24 (1986), 188--196.
,
J. of Number Theory, 24 (1986), 188--196.
[1] [2]
- 4
- K.S. Davis and W.A. Webb, Lucas' Theorem for prime powers,
Europ. J. Combinatorics, 11 (1990), 229--233.
[1]
- 5
- L.E. Dickson, Divisibility of Factorials and Multinomial
Coefficients, Chapter XI in `History of the Theory of Numbers', Vol.I,
(Chelsea, New York, 1919).
[1] [2]
- 6
- R.D. Fray, Congruence Properties of Ordinary and q-Binomial
Coefficients, Duke Math. J., 34 (1967), 467--480.
[1]
- 7
- I. Gessel, Some Congruences for the Apéry numbers,
J. of Number Theory, 14 (1982), 362--368.
[1]
- 8
- A. Granville, Zaphod Beeblebrox's brain and the fifty--ninth
row of Pascal's Triangle, Amer. Math. Monthly, 99 (1992), 318--381.
[1] [2] [3]
- 9
- R.K. Guy, Reviews in Number Theory, (Amer. Math. Soc.,
Rhode Island, 1984).
[1]
- 10
- R.H. Hudson and K.S. Williams,
Binomial Coefficients and Jacobi Sums,
Trans. Amer. Math. Soc., 281 (1984), 431--505.
[1]
- 11
- J.P. Jones, D. Sato, H. Wada and D. Wiens,
Diophantine representation of the set of prime numbers,
Amer. Math. Monthly, 83 (1976), 449--464.
[1]
- 12
- D. E. Knuth and H. S. Wilf, The power of a prime
that divides a generalized binomial coefficient, J. reine angew. Math.,
396 (1989), 212-219.
[1]
- 13
- E. Lehmer, On congruences involving Bernoulli numbers and the
quotients of Fermat and Wilson,
Annals of Math., 39 (1938), 350--360.
- 14
- W.J. Leveque, Reviews in Number Theory, (Amer. Math. Soc.,
Rhode Island, 1974).
[1]
- 15
- C. T. Long, Pascal's triangle modulo p, Fib. Quart.,
19 (1981), 458-463.
[1]
- 16
- B. Mandelbrot, The Fractal Geometry of Nature, (Freeman,
San Francisco, 1982).
[1]
- 17
- H.B. Mann and D.S. Shanks, A neccessary and sufficient
condition for primality, and its source,
J. of Comb. Theory Ser. A, 13 (1972), 131--134.
[1]
- 18
- F. Morley, Note on the congruence
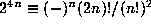 , where 2n+1 is a prime,
Annals of Math., 9 (1895), 168--170.
, where 2n+1 is a prime,
Annals of Math., 9 (1895), 168--170.
[1]
- 19
- D. Singmaster, Divisibility of binomial and multinomial
coefficients by primes and prime powers, in `A collection of manuscripts
related to the Fibonacci sequence', (Fib. Assoc., Santa Clara, 1980), 98--113.
[1] [2]
- 20
- K.B. Stolarsky, Power and Exponential sums of digit sums
related to binomial coefficient parity, SIAM J. Appl. Math., 32
(1977), 717--730.
[1] [2]
- 21
- L.C. Washington, Introduction to Cyclotomic Fields,
(Springer--Verlag, New York, 1982).
[1] [2] [3]
- 22
- S. Wolfram, Geometry of Binomial Coefficients, American Math. Monthly, 91 (1984), 566-571.
[1]
![[Shownotes]](../gif/annotate/shide-151.gif)
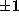 's defined by binary patterns,
Diss. Math., 283, 60pp.
's defined by binary patterns,
Diss. Math., 283, 60pp. 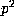 determination of
determination of 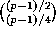 ,
J. of Number Theory, 24 (1986), 188--196.
,
J. of Number Theory, 24 (1986), 188--196.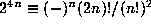 , where 2n+1 is a prime,
Annals of Math., 9 (1895), 168--170.
, where 2n+1 is a prime,
Annals of Math., 9 (1895), 168--170.