![[Shownotes]](../gif/annotate/shide-31.gif)
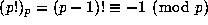 ,
may be generalized to prime powers as follows:
,
may be generalized to prime powers as follows:
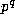 we have
we have

 where
where 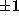 is as in Theorem 1.
is as in Theorem 1.
This was proved by Gauss in Disquisitiones Arithmeticae,
as follows:\
If we pair up each m in the product with its inverse 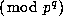 then we see that
then we see that 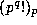 is congruent, modulo
is congruent, modulo 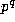 , to the product of
those
, to the product of
those 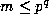 that are not distinct from their inverses
that are not distinct from their inverses 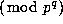 ,
that is those m for which
,
that is those m for which 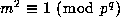 . It is
easy to show that the only such m are 1 and
. It is
easy to show that the only such m are 1 and 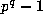 unless
unless 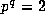 (when one only has m=1) or
(when one only has m=1) or 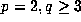 when one has the additional
solutions
when one has the additional
solutions 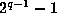 and
and 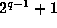 . The result follows.
. The result follows.
We may deduce from Lemma 1 the following
Corollary 1. For any given prime power 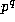 let
let 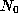 be the least non-negative residue of
be the least non-negative residue of 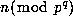 .
Then
.
Then

 where
where 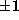 is as in Theorem 1.
is as in Theorem 1.
Proof: Write each r in the product below as 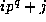 , to get
, to get

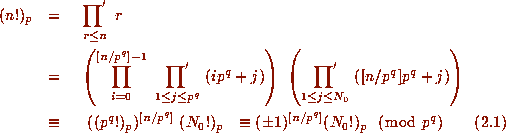 by Lemma 1, where
by Lemma 1, where 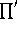 signifies
a product over integers not divisible by p.
signifies
a product over integers not divisible by p.
In 1808 Legendre showed that the exact power of p dividing 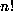 is
is

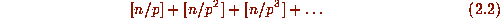 Writing n in base p as above, we define the sum of digits function
Writing n in base p as above, we define the sum of digits function
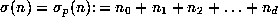 . Then (2.2)
equals
. Then (2.2)
equals

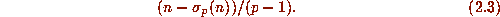 These are both easily proved by an induction hypothesis: If n<p
(that is
These are both easily proved by an induction hypothesis: If n<p
(that is 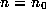 ) then clearly p does not divide
) then clearly p does not divide 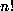 and both (2.2) and
(2.3) equal zero. So, given
and both (2.2) and
(2.3) equal zero. So, given 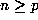 , note that the set of integers
, note that the set of integers 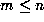 that are divisible by p are precisely the set of integers pk for
that are divisible by p are precisely the set of integers pk for
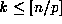 . Thus the power of p dividing
. Thus the power of p dividing 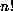 is exactly
is exactly 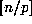 plus the power of p dividing
plus the power of p dividing 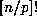 . (2.2) then follows immediately
from the induction hypothesis, and (2.3) after noting that
. (2.2) then follows immediately
from the induction hypothesis, and (2.3) after noting that

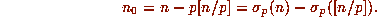
Let r = n-m and write each of
n, m and r in base p. Let 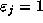 if there is a `carry'
in the jth digit when adding m and r in base p, let
if there is a `carry'
in the jth digit when adding m and r in base p, let
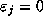 otherwise (including
otherwise (including 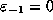 ).
We use (2.3) to deduce
).
We use (2.3) to deduce
Kummer's Theorem. The power to which prime
p divides the binomial coefficient 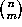 is given
by the number of `carries' when we add m and n-m in base p.
is given
by the number of `carries' when we add m and n-m in base p.
Proof:
One can easily check that, for each integer 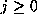 ,
,

 Now, by (2.3), the power of p dividing
Now, by (2.3), the power of p dividing 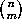 is
is

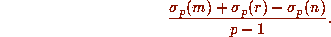 By definition, this equals
By definition, this equals

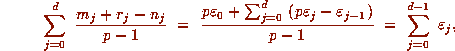 the total number of `carries'.
the total number of `carries'.
By a similar argument we also have, for each 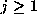 , that
, that

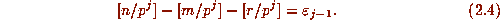 This can be seen by letting
This can be seen by letting 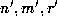 be the least residues, in absolute
value, of
be the least residues, in absolute
value, of 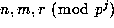 , respectively, so that
, respectively, so that 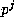 times the
left side of (2.4), plus
times the
left side of (2.4), plus 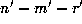 equals n-m-r = 0. However,
equals n-m-r = 0. However,

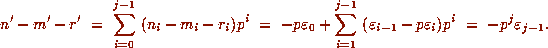 and (2.4) follows.
and (2.4) follows.
The improvement, (1.2), of Lucas' Theorem is easily deduced from the equation

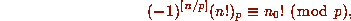 which was discovered by Anton, Stickelberger and then Hensel.
For an arbitrary prime power
which was discovered by Anton, Stickelberger and then Hensel.
For an arbitrary prime power 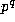 , this may be generalized
as follows:
, this may be generalized
as follows:
With definitions as in Theorem 1, we have, for any given 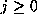 ,
,

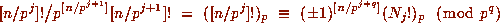 by Corollary 1. Multiplying together this congruence for each
by Corollary 1. Multiplying together this congruence for each 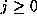 we get
we get
Proposition 1. For any integer n and prime power 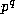 ,
we have
,
we have

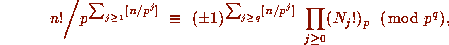 where
where 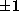 and each
and each 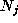 are as in Theorem 1.
are as in Theorem 1.
Theorem 1 then follows from dividing the equation in Proposition 1 by
the corresponding ones for m and r, and then using (2.4) to sort
out the exponents of 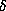 and p.
and p.