![[Shownotes]](../gif/annotate/sshow-61.gif)
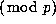 by
such a
`pictorial approach':
by
such a
`pictorial approach':
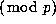 has 1's on either end with 0's all the way in--between;
and from the fact that any entry of the triangle is just the sum
of the two adjacent entries on the line immediately above,
we form a triangle underneath each of these 1's whose entries
are the same as those of Pascal's triangle
has 1's on either end with 0's all the way in--between;
and from the fact that any entry of the triangle is just the sum
of the two adjacent entries on the line immediately above,
we form a triangle underneath each of these 1's whose entries
are the same as those of Pascal's triangle 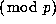 .
These two triangles stay independent of one another
until they meet in the 2pth row. Thus, in that row, we have two copies
of the pth row of Pascal's triangle, side--by--side, except that the
middle term, has the corner terms of our two triangles overlayed:
Therefore this row has a 1 on either end, a 2 in the middle, and 0's
all the way in--between.
.
These two triangles stay independent of one another
until they meet in the 2pth row. Thus, in that row, we have two copies
of the pth row of Pascal's triangle, side--by--side, except that the
middle term, has the corner terms of our two triangles overlayed:
Therefore this row has a 1 on either end, a 2 in the middle, and 0's
all the way in--between.
Again, underneath each of these 1's we form a triangle whose entries
are the same as those of Pascal's triangle 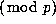 , while underneath
the 2 we form a triangle whose entries are twice that in Pascal's triangle
, while underneath
the 2 we form a triangle whose entries are twice that in Pascal's triangle 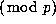 .
These three triangles meet in the 3pth row, which thus
has 1's on either end, 3's at one--third and two--thirds of the way
across and 0's everywhere else.
Now underneath each of the 1's we again form a triangle whose entries
are the same as those of Pascal's triangle
.
These three triangles meet in the 3pth row, which thus
has 1's on either end, 3's at one--third and two--thirds of the way
across and 0's everywhere else.
Now underneath each of the 1's we again form a triangle whose entries
are the same as those of Pascal's triangle 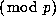 , while underneath
the 3's we form a triangle whose entries are three times
that in Pascal's triangle
, while underneath
the 3's we form a triangle whose entries are three times
that in Pascal's triangle 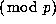 .
.
Continuing this process, we see that the npth row of Pascal's triangle
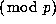 is a copy of the nth row, with
is a copy of the nth row, with
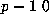 's placed between consecutive entries;
and that the p-1 rows immediately beneath the npth row are given by
forming triangles underneath each non--zero entry of the npth row
(say,
's placed between consecutive entries;
and that the p-1 rows immediately beneath the npth row are given by
forming triangles underneath each non--zero entry of the npth row
(say, 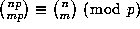 ),
that are
),
that are 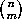 times Pascal's triangle
times Pascal's triangle 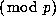 .
Thus
.
Thus 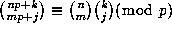 ,
so that Lucas' Theorem may be viewed as a result about automata with
p possible states !
,
so that Lucas' Theorem may be viewed as a result about automata with
p possible states !
Wolfram gave an elegant proof of Glaisher's Theorem (that the number of odd
entries in a given row of Pascal's triangle is a power of 2),
via the following induction hypothesis: For each 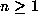 , rows
, rows 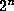 to
to
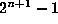 modulo 2 are given by taking two copies of rows 0 to
modulo 2 are given by taking two copies of rows 0 to
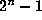 of Pascal's triangle, modulo 2, side--by--side, and filling
the space in--between with 0's; moreover Glaisher's result holds for
each of these rows.
For n=1 we observe this by computation.
For
of Pascal's triangle, modulo 2, side--by--side, and filling
the space in--between with 0's; moreover Glaisher's result holds for
each of these rows.
For n=1 we observe this by computation.
For 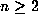 note that row
note that row 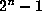 must be all 1's
so that row
must be all 1's
so that row 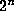 has 1's on either end with 0's all the way in--between.
Thus, underneath each of these 1's we obtain a triangle whose entries
are the same as those of Pascal's triangle, and the triangles don't meet
until after the
has 1's on either end with 0's all the way in--between.
Thus, underneath each of these 1's we obtain a triangle whose entries
are the same as those of Pascal's triangle, and the triangles don't meet
until after the 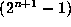 th row.
Therefore the
th row.
Therefore the 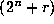 th row (
th row (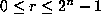 ) modulo 2 is just two
copies of the rth row modulo 2, with some 0's in--between,
and so has twice as many odd entries as the rth row; this
completes the proof.
) modulo 2 is just two
copies of the rth row modulo 2, with some 0's in--between,
and so has twice as many odd entries as the rth row; this
completes the proof.
Also, as row 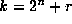 is two copies of row r, whose first entries
are seperated by
is two copies of row r, whose first entries
are seperated by 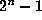 0's, thus Roberts' integer
0's, thus Roberts' integer

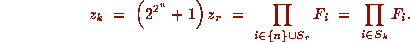
The above approach has a further pretty consequence (see also [15]):
If we cut Pascal's triangle modulo p into subtriangles whose boundaries
have 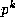 entries, in the obvious way (that is, with rows 0 to
entries, in the obvious way (that is, with rows 0 to 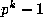 in the first such triangle, then rows
in the first such triangle, then rows 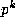 to
to 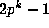 cut into
three subtriangles, two outer and one inner inverted triangle, etc. etc.),
then any given subtriangle is exactly the sum of the
two adjacent subtriangles, in the row of subtriangles immediately above.
In other words these subtriangles obey the same addition law as Pascal's
triangle itself. The behaviour of Pascal's triangle modulo higher powers of
p is somewhat more complicated, but still follows certain rules which
are discussed in [8].
cut into
three subtriangles, two outer and one inner inverted triangle, etc. etc.),
then any given subtriangle is exactly the sum of the
two adjacent subtriangles, in the row of subtriangles immediately above.
In other words these subtriangles obey the same addition law as Pascal's
triangle itself. The behaviour of Pascal's triangle modulo higher powers of
p is somewhat more complicated, but still follows certain rules which
are discussed in [8].
Finally we mention a result of Trollope (1968): \
Let 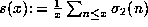 .
A typical integer
.
A typical integer 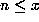 has
has 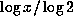 digits, half of
which one expects to be 1's, so that
digits, half of
which one expects to be 1's, so that 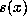 should be
approximately
should be
approximately 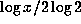 . Therefore, we compare
. Therefore, we compare 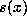 with
with
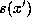 , when
, when 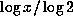 and
and 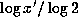 have the same
fractional part, by considering the function
have the same
fractional part, by considering the function

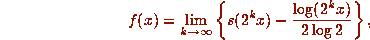 for each
for each 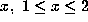 .
One can easily show that this limit exists and
that the function
.
One can easily show that this limit exists and
that the function 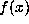 is continuous. However Trollope
proved the surprising result that
is continuous. However Trollope
proved the surprising result that 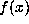 is nowhere differentiable.
For more on such questions see [2].
is nowhere differentiable.
For more on such questions see [2].