The aim of this section is to generalize to the cubic case the well known
correspondence between binary quadratic forms and quadratic number fields.
These results are due to Davenport and Heilbronn (see [5] and [6]).
Before stating and proving the main theorem, we need a few preliminary
results. We let 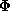 be the set of classes of primitive irreducible binary
cubic forms. This makes sense, thanks to Proposition 1.2.
be the set of classes of primitive irreducible binary
cubic forms. This makes sense, thanks to Proposition 1.2.
 Annotation Form Interface
Annotation Form Interface
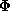 be the set of classes of primitive irreducible binary
cubic forms. This makes sense, thanks to Proposition 1.2.
be the set of classes of primitive irreducible binary
cubic forms. This makes sense, thanks to Proposition 1.2.