- Step 1 will in practice not be necessary since we will always
use this algorithm with reduced forms (see later), which are
automatically irreducible when they belong to U.
- Although Step 2 seems to be necessary, this is in fact not the case
since nonprimitive forms will be excluded in the subsequent steps. Indeed,
let p be a prime dividing all the coefficients of F. Then clearly
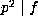 . If p>3, Step 4 will return false. Assume now p=2
or p=3. Then
. If p>3, Step 4 will return false. Assume now p=2
or p=3. Then 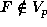 and F has at least a double root modulo p.
If F has only a double and not a triple root, then
and F has at least a double root modulo p.
If F has only a double and not a triple root, then 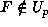 . On the
other hand if F has a triple root, i.e if
. On the
other hand if F has a triple root, i.e if 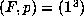 then
then
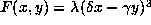 with
with 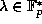 and
hence
and
hence 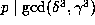 so
so 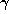 and
and 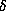 are equal to
zero modulo p, hence
are equal to
zero modulo p, hence 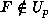 .
.
- Even though it seems useful to include the unnecessary Step 2, it
can be shown that on average it slows the algorithm, so in the
final form thanks to the preceding remark we will suppress it.
 Annotation Form Interface
Annotation Form Interface
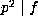 . If p>3, Step 4 will return false. Assume now p=2
or p=3. Then
. If p>3, Step 4 will return false. Assume now p=2
or p=3. Then 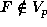 and F has at least a double root modulo p.
If F has only a double and not a triple root, then
and F has at least a double root modulo p.
If F has only a double and not a triple root, then 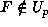 . On the
other hand if F has a triple root, i.e if
. On the
other hand if F has a triple root, i.e if 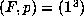 then
then
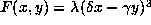 with
with 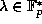 and
hence
and
hence 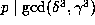 so
so 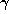 and
and 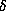 are equal to
zero modulo p, hence
are equal to
zero modulo p, hence 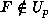 .
.