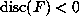, i.e when F corresponds to
a complex cubic field. In this case the Hessian is an indefinite quadratic
form, and in general there will be many reduced quadratic forms equivalent
to it. Instead of using the Hessian, we will use a clever idea due to Matthews
and Berwick (see [9]). If 
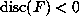, then F has a unique real root 
,
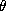and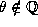 
if F is irreducible, so if we factor F in 
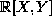as
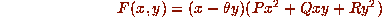the quadratic form 
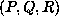will be definite ( i.e 
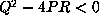), but with
real nonrational coefficients. We are going to show that the form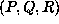 
has many of the properties of the Hessian.
Annotation Form Interface