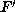 be two reduced cubic forms and
be two reduced cubic forms and 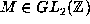 such
that
such
that 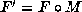 . Then
. Then 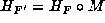 and since
and since 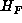 and
and 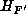 are
reduced, it follow from Lemma 5.2 that
are
reduced, it follow from Lemma 5.2 that 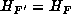 and that M is an
automorphism of
and that M is an
automorphism of 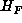 . We now have only a finite number of possibilities
(exactly 16) to test for M. Let
. We now have only a finite number of possibilities
(exactly 16) to test for M. Let 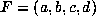 .
.
First, if 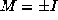 , we have
, we have 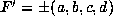 hence the conditions a>0 on
F and
hence the conditions a>0 on
F and 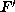 imply M=I.
imply M=I.
If P=R and 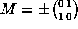 , we have
, we have 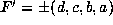 hence the conditions
hence the conditions 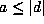 on F and
on F and 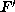 imply a=|d|, hence the
additional conditions |b|<|c| on F and
imply a=|d|, hence the
additional conditions |b|<|c| on F and 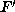 give a contradiction.
give a contradiction.
In the case P=R and Q=0 and 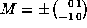 , then we
have
, then we
have 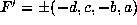 , and the conditions
, and the conditions 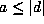 on F and
on F and 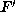 imply a=|d| and the additional conditions |b|<|c| also lead to
a contradiction. Note that an easy calculation shows that in this case
imply a=|d| and the additional conditions |b|<|c| also lead to
a contradiction. Note that an easy calculation shows that in this case
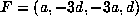 .
.
If P=Q and 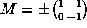 , we have
, we have
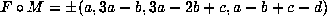 and hence the conditions
|b|<|3a-b| on F and
and hence the conditions
|b|<|3a-b| on F and 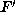 give a contradiction.
give a contradiction.
If Q=0 and 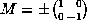 , we have
, we have
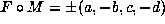 and hence the conditions b>0 on F and
and hence the conditions b>0 on F and 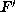 give a contradiction.
give a contradiction.
Finally assume that P=Q=R and M is one of the six matrices given by
Lemma 5.2. Then an easy computation shows that F is of the form
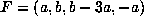 . The reducedness of F is equivalent to a>0, |b|<|3a-b|.
For the six matrices of Lemma 5.2, we have respectively
. The reducedness of F is equivalent to a>0, |b|<|3a-b|.
For the six matrices of Lemma 5.2, we have respectively
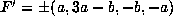 ,
, 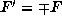 and
and 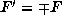 . The first two leads to a
contradiction because of the condition |b|<|3a-b|, and the other four
together with a>0 imply
. The first two leads to a
contradiction because of the condition |b|<|3a-b|, and the other four
together with a>0 imply 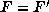 , and the matrices
, and the matrices
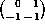 and
and
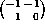 as
automorphisms of F. Thus in this case, and only in this case, the
automorphism group of F is nontrivial and is cyclic of order 3 generated
by one of the above two matrices. This finishes the proof of (1).
as
automorphisms of F. Thus in this case, and only in this case, the
automorphism group of F is nontrivial and is cyclic of order 3 generated
by one of the above two matrices. This finishes the proof of (1).
(2) Let 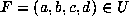 be a reducible real cubic form. We will
successively replace F by equivalent forms, which we will still denote
be a reducible real cubic form. We will
successively replace F by equivalent forms, which we will still denote
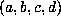 by abuse of notation, until we can conclude. Set
by abuse of notation, until we can conclude. Set 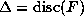 .
Assume by contradiction that F is reducible. Then by transforming F by
a suitable element of
.
Assume by contradiction that F is reducible. Then by transforming F by
a suitable element of 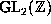 we may assume that a=0 and hence
we may assume that a=0 and hence 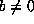 since
since 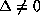 . By changing if necessary F into -F, we may assume
that
. By changing if necessary F into -F, we may assume
that 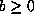 . Changing
. Changing 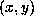 into
into 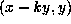 for a suitable k, we may
assume that
for a suitable k, we may
assume that 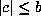 and finally by changing if necessary
and finally by changing if necessary 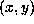 into
into
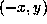 , we may assume
, we may assume 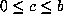 . We thus have
. We thus have 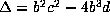 ,
and
,
and 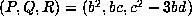 .
.
Let p be an odd prime dividing b. Since 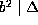 , we have
, we have
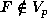 , but since
, but since 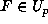 , by definition this means that
, by definition this means that
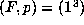 plus an additional condition. In particular, by
Proposition 3.3 (2) we have
plus an additional condition. In particular, by
Proposition 3.3 (2) we have 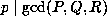 , hence
, hence 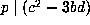 , so
, so
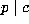 , hence
, hence 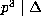 , and this leads to a contradiction unless
p=3 by Proposition 3.3 (3). But if p=3, we have a=0 hence
, and this leads to a contradiction unless
p=3 by Proposition 3.3 (3). But if p=3, we have a=0 hence 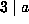 and
and
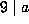 so Proposition 3.3 (4) implies that
so Proposition 3.3 (4) implies that 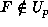 , contradiction
again.
, contradiction
again.
There remains the case of p=2 dividing b. In that case we have
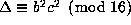 hence
hence
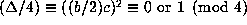 , so
, so 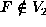 .
Since
.
Since 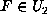 , we have
, we have 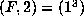 . We conclude as before by Proposition
3.3 (2) that
. We conclude as before by Proposition
3.3 (2) that 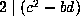 , hence
, hence 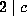 hence
hence 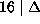 , in
contradiction with
, in
contradiction with 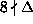 coming from Proposition 3.3 (3).
coming from Proposition 3.3 (3).
We deduce from the different cases above that b=1, and hence c=0 or
c=1. Hence if we call G the final cubic form that we have obtained,
we have 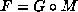 for a certain
for a certain 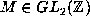 , and
, and 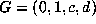 with c=0 or 1. Hence
with c=0 or 1. Hence 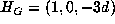 or
or 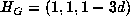 . Since
these are reduced quadratic forms equivalent to
. Since
these are reduced quadratic forms equivalent to 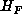 which is reduced,
we have
which is reduced,
we have 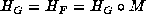 . Now, since d<0 (otherwise
. Now, since d<0 (otherwise 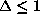 and
and
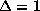 is impossible), the only automorphisms of
is impossible), the only automorphisms of 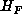 are
are 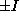 , and
since we must have a>0, this implies M=I hence F=G, contradiction.
, and
since we must have a>0, this implies M=I hence F=G, contradiction.
(3) The uniqueness statement follows from (1). Let 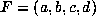 be an
irreducible real cubic form and
be an
irreducible real cubic form and 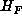 its Hessian. By the usual theory of
reduction of quadratic forms (with the added twist that matrices of determinant
-1 are allowed), we can find
its Hessian. By the usual theory of
reduction of quadratic forms (with the added twist that matrices of determinant
-1 are allowed), we can find 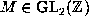 such that
such that 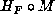 is
reduced, hence by changing F into
is
reduced, hence by changing F into 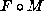 we may assume
we may assume 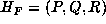 reduced.
reduced.
In all the cases of Definition 5.3, it is easily checked that the use of the 16 matrices of Lemma 5.2 will lead to a reduced form. Note that it is essential to assume F irreducible, otherwise the result would be false. More precisely, it is enough to check that the forms with a=0, or b=0 when Q=0, or |b|=|3a-b| when P=Q or a=|d| and |b|=|c| when P=R are all reducible. This finishes the proof of the proposition.