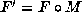 where F and
where F and 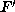 are reduced and
are reduced and
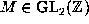 . Then by the formula proved above, there exists
. Then by the formula proved above, there exists 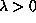 such that
such that 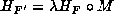 . As before, we deduce from the
inequalities |Q|<P<R and
. As before, we deduce from the
inequalities |Q|<P<R and 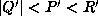 that
that 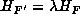 , and hence
that M is an automorphism of
, and hence
that M is an automorphism of 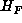 . The proof then terminates as in the real
case, except that there are no special cases to consider since the forms are
irreducible.
. The proof then terminates as in the real
case, except that there are no special cases to consider since the forms are
irreducible.
(2) As in the real case, a complex reducible form F belonging to U must
be equivalent to 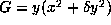 or to
or to 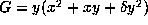 with
with
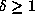 . If
. If 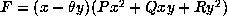 and
and 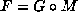 with
with
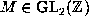 , then
, then 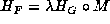 for some
for some 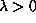 .
Hence the reduced form
.
Hence the reduced form 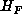 is equivalent to a multiple of
is equivalent to a multiple of 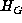 with
with
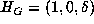 or
or 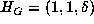 respectively which are also reduced,
and hence it is equal to that multiple, hence we have either Q=0 or
Q=P for the form F, which are both excluded from the definition of a
reduced form in the complex case.
respectively which are also reduced,
and hence it is equal to that multiple, hence we have either Q=0 or
Q=P for the form F, which are both excluded from the definition of a
reduced form in the complex case.
(3) is clear: we can always reduce first 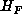 by an element of
by an element of 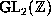 so that it satisfies 0<|Q|<P<R, the strict inequalities being guaranteed by
the irreducibility of F. We must have
so that it satisfies 0<|Q|<P<R, the strict inequalities being guaranteed by
the irreducibility of F. We must have 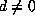 otherwise F is reducible,
and since P=a, we have a>0. Changing
otherwise F is reducible,
and since P=a, we have a>0. Changing 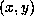 into
into
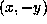 if necessary (which changes Q into -Q and leave P and R
unchanged), we may also assume that
if necessary (which changes Q into -Q and leave P and R
unchanged), we may also assume that 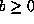 . Finally, if b=0,
changing again
. Finally, if b=0,
changing again 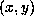 into
into 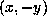 of necessary we may assume d>0
since
of necessary we may assume d>0
since 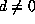 .
.