The unique solution in the
antifunnel,
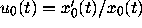 , has the value
, has the value 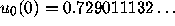 . (This is what a standard fourth-order Runge-Kutta
approximation will give if you solve backwards from t=-9,u=3 or from
. (This is what a standard fourth-order Runge-Kutta
approximation will give if you solve backwards from t=-9,u=3 or from
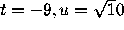 ; these points are on the top and the bottom of the
antifunnel, and thus should give upper and lower bounds for
; these points are on the top and the bottom of the
antifunnel, and thus should give upper and lower bounds for 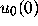 . An
error analysis done as in [4, chapter 3], and helped by the program
Numerical Methods from MacMath, shows that all written decimal
digits of
. An
error analysis done as in [4, chapter 3], and helped by the program
Numerical Methods from MacMath, shows that all written decimal
digits of 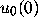 are correct.) Thus a numerical solution of
are correct.) Thus a numerical solution of
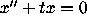 , backward in time, starting with
, backward in time, starting with
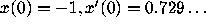 , remains bounded for a
considerable length of time, as our computer experiments showed---but
eventually it will blow up, since the exact solution
, remains bounded for a
considerable length of time, as our computer experiments showed---but
eventually it will blow up, since the exact solution 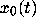 is
unstable as
is
unstable as 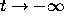 .
.
 Annotation Form Interface
Annotation Form Interface
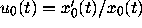 , has the value
, has the value 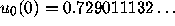 . (This is what a standard fourth-order Runge-Kutta
approximation will give if you solve backwards from t=-9,u=3 or from
. (This is what a standard fourth-order Runge-Kutta
approximation will give if you solve backwards from t=-9,u=3 or from
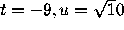 ; these points are on the top and the bottom of the
antifunnel, and thus should give upper and lower bounds for
; these points are on the top and the bottom of the
antifunnel, and thus should give upper and lower bounds for 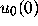 . An
error analysis done as in [4, chapter 3], and helped by the program
Numerical Methods from MacMath, shows that all written decimal
digits of
. An
error analysis done as in [4, chapter 3], and helped by the program
Numerical Methods from MacMath, shows that all written decimal
digits of 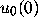 are correct.) Thus a numerical solution of
are correct.) Thus a numerical solution of
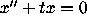 , backward in time, starting with
, backward in time, starting with
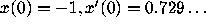 , remains bounded for a
considerable length of time, as our computer experiments showed---but
eventually it will blow up, since the exact solution
, remains bounded for a
considerable length of time, as our computer experiments showed---but
eventually it will blow up, since the exact solution 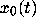 is
unstable as
is
unstable as 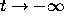 .
.