The solutions on the right of Figure  are merging (far offscreen) as
are merging (far offscreen) as 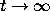 ,
and they are ``straight'' enough to try using the
theory of fences and funnels.
In fact, as a result of Condition II, we see from equation (12) that as
,
and they are ``straight'' enough to try using the
theory of fences and funnels.
In fact, as a result of Condition II, we see from equation (12) that as
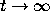 , solutions are going to behave very much like solutions to
the equation
, solutions are going to behave very much like solutions to
the equation 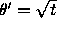 . To be precise, from (12) we get
. To be precise, from (12) we get

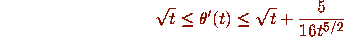 for all t > 0. Therefore, for any C, the curves
for all t > 0. Therefore, for any C, the curves

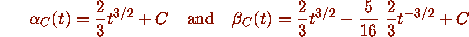 are respectively a lower fence and an upper fence for the differential
equation (12). That is, for every t>0 the slope
are respectively a lower fence and an upper fence for the differential
equation (12). That is, for every t>0 the slope 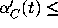 the slope of the direction field for
the slope of the direction field for 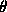 at that point, and
at that point, and
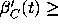 the slope of the direction field. Together these fences
define an antifunnel
the slope of the direction field. Together these fences
define an antifunnel
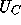 , which is narrowing as
, which is narrowing as 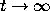 ; see Figure
; see Figure  .
We will show in Appendix C that there is exactly one solution
.
We will show in Appendix C that there is exactly one solution
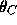 which is trapped in the narrowing antifunnel
which is trapped in the narrowing antifunnel 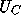 for all
t>0, and that every solution of (12) for t > 0 is of this form for
some C.
for all
t>0, and that every solution of (12) for t > 0 is of this form for
some C.
 Annotation Form Interface
Annotation Form Interface
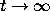 ,
and they are ``straight'' enough to try using the
theory of fences and funnels.
In fact, as a result of Condition II, we see from equation (12) that as
,
and they are ``straight'' enough to try using the
theory of fences and funnels.
In fact, as a result of Condition II, we see from equation (12) that as
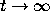 , solutions are going to behave very much like solutions to
the equation
, solutions are going to behave very much like solutions to
the equation 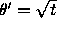 . To be precise, from (12) we get
. To be precise, from (12) we get

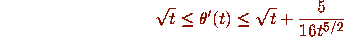 for all t > 0. Therefore, for any C, the curves
for all t > 0. Therefore, for any C, the curves

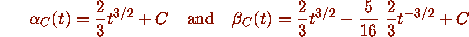 are respectively a lower fence and an upper fence for the differential
equation (12). That is, for every t>0 the slope
are respectively a lower fence and an upper fence for the differential
equation (12). That is, for every t>0 the slope 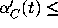 the slope of the direction field for
the slope of the direction field for 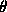 at that point, and
at that point, and
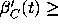 the slope of the direction field. Together these fences
define an antifunnel
the slope of the direction field. Together these fences
define an antifunnel
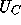 , which is narrowing as
, which is narrowing as 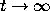 ; see Figure
; see Figure 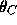 which is trapped in the narrowing antifunnel
which is trapped in the narrowing antifunnel 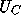 for all
t>0, and that every solution of (12) for t > 0 is of this form for
some C.
for all
t>0, and that every solution of (12) for t > 0 is of this form for
some C.