The 3x+1 Conjecture is simple to state and apparently intractably hard
to solve.
It shares these properties with other iteration problems, for example
that of aliquot sequences (see Guy [36], Problem B6)
and with celebrated Diophantine equations such as Fermat's last theorem.
Paul Erdös commented concerning the intractability of the
3x+1 problem: ``Mathematics is not yet ready for such problems.''
Despite this doleful pronouncement, study of the 3x+1 problem has not been
without reward.
It has interesting connections with the Diophantine approximation of
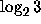 and the distribution
and the distribution 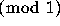 of the sequence
of the sequence
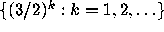 , with questions of ergodic
theory on the 2-adic integers
, with questions of ergodic
theory on the 2-adic integers 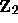 , and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
, and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
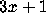 problem and survey all the literature I am aware of
about this problem and its generalizations.
problem and survey all the literature I am aware of
about this problem and its generalizations.
 Annotation Form Interface
Annotation Form Interface
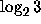 and the distribution
and the distribution 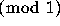 of the sequence
of the sequence
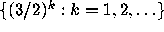 , with questions of ergodic
theory on the 2-adic integers
, with questions of ergodic
theory on the 2-adic integers 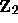 , and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
, and with computability theory ---
a generalization of the 3x+1 problem has been shown to be a computationally
unsolvable problem.
In this paper I describe the history of the
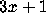 problem and survey all the literature I am aware of
about this problem and its generalizations.
problem and survey all the literature I am aware of
about this problem and its generalizations.