The exact origin of the 3x+1 problem is obscure.
It has circulated by word of mouth in the mathematical community for
many years.
The problem is traditionally credited to Lothar Collatz,
at the University of Hamburg.
In his student days in the 1930's, stimulated by the lectures of
Edmund Landau, Oskar Perron, and Issai Schur,
he became interested in number-theoretic functions.
His interest in graph theory led him to the idea of representing such
number-theoretic functions as directed graphs, and questions about the
structure of such graphs are tied to the behavior of iterates of such
functions [25].
In his notebook dated July 1, 1932, he considered the function

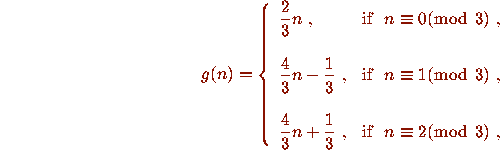 which
gives rise to a permutation P of the natural numbers
which
gives rise to a permutation P of the natural numbers

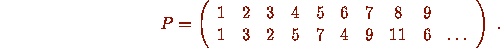 He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates
He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates 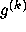 (8) remain
bounded or are unbounded [24].
I will call the study of the iterates of
(8) remain
bounded or are unbounded [24].
I will call the study of the iterates of 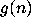 the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning
the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning 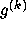 (8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the
(8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the 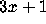 problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].
problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].
 Annotation Form Interface
Annotation Form Interface

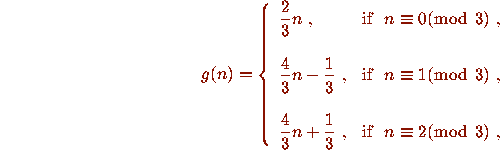 which
gives rise to a permutation P of the natural numbers
which
gives rise to a permutation P of the natural numbers

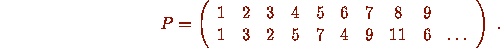 He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates
He posed the problem of determining the cycle structure of P, and asked in
particular
whether or not the cycle of this permutation containing 8 is
finite or infinite ,
i.e., whether or not the iterates 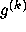 (8) remain
bounded or are unbounded [24].
I will call the study of the iterates of
(8) remain
bounded or are unbounded [24].
I will call the study of the iterates of 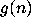 the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning
the
original Collatz problem.
Although Collatz never published any of his iteration problems,
he circulated them at the International Congress of
Mathematicians in 1950 in Cambridge,
Massachusetts, and eventually the original Collatz problem appeared in
print ([9], [47], [62]).
His original question concerning 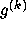 (8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the
(8) has never been answered;
the cycle it belongs to is believed to be infinite.
Whatever its exact origins, the 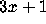 problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].
problem was certainly known to the
mathematical community by the early 1950's; it was
discovered in 1952 by B. Thwaites [72].