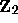Ergodic theory is concerned with the extent to which iterates of a function mix subsets of a measure space. I will use the following basic concepts of ergodic theory specialized to the measure space

with the measure

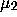. A measure-preserving function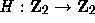

is ergodic if the only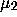

-measurable sets E for which

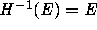are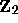

and the empty set, i.e., such a function does such a good job of mixing points in the space that it has no nontrivial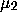

-invariant sets. It can be shown [[39], p. 36] that an equivalent condition for ergodicity is that

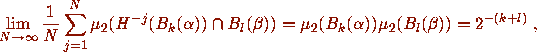for all

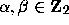and all integers

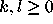. This condition in turn is equivalent to the assertion that for almost all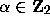

the sequence of iterates

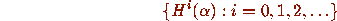is uniformly distributed

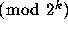for all

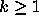. A function

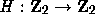is strongly mixing if

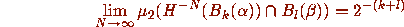for all

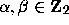and all

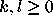. Strongly mixing functions are ergodic.

Annotation Form Interface
Your name: E-Mail address: Annotation Subject: Related URL: