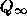under iteration is itself of interest.
Let 
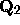denote the set of all rational numbers having odd
denominators, so tha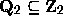t 
.
The set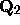 
consists of exactly those 2-adic integers whose 2-adic expansion is finite
or eventually periodic.
The Finite Cycles Conjecture is equivalent to the assertion that there is a finite
odd integer M such that
In fact one can take 
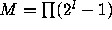, where the product runs
over all integers l for which there is a cycle of minimal length l.
As a hypothesis for further work I advance the following conjecture.
Annotation Form Interface