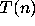Several authors have investigated the range of validity of the result that has a finite stopping time for almost all integers n by considering more general classes of periodicity linear functions. One such class 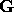consists of all functions 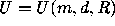which are given by

 

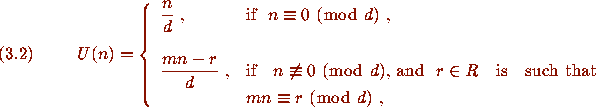where m and d are positive integers with 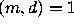and 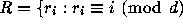, 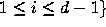is a fixed set of residue class representatives of the nonzero residue classes 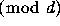. The 3x+1 function T is in the class 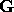. H. Möller [54] completely characterized the functions 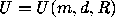in the set 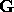which have a finite stopping time for almost all integers n. He showed they are exactly those functions for which

 

E. Heppner [41] proved the following quantitative version of this result, thereby generalizing Theorem D.